Piecewise functions in matlab
Alec Jacobson
June 15, 2010
Not the most difficult thing to do by any means. But here's a handy conversion from a math formula to matlab. Say you have the piecewise polynomial, m, defined as:
/ 0 if x < 0,
m(x) = | -2x²(x - 3/2) if 0 ≤ x < 1,
| 1 + (x - 1) if 1 ≤ x < 3/2,
\ x - 1/4 if x ≥ 3/2.
So in matlab if I have some variable x with some values, i.e.
x = -1:0.01:2;
then I can formulate the above as:
m = ...
(0 ) .* (x < 0 ) + ...
(-2*x.^2.*(x-3/2)) .* (0 <= x & x < 1 ) + ...
(1+(x-1).^2 ) .* (1 <= x & x < 3/2) + ...
(x-1/4 ) .* (x >= 3/2 );
Now, I can show a plot:
plot(x,m);
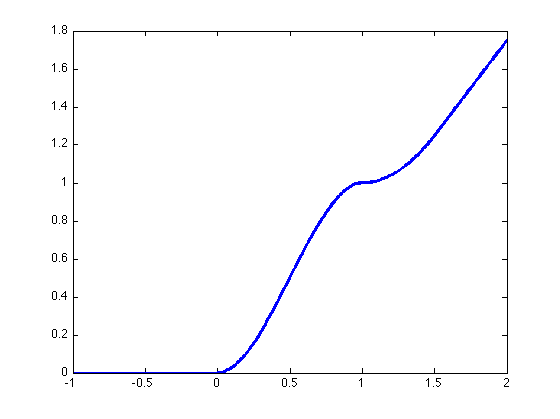
This works because the conditions in matlab are now logicals that return a vector the same size as x, with 1's if the condition was true and 0's otherwise. Multiplied against the value for the condition and added to the next gives the correct solution. I guess this method is somewhat risky in the sense that if you mess up your logicals or inequalities the addition could sum up erroneous values without recognizing the error. But I think the presentation is very nice and is easily broken up if need be.
Note: The polynomial above is from Higher Order Barycentric Coordinates by Torsten Langer and Hans-Peter Seidel.

