Barycentric versus voronoi regional area in mass matrices
Alec Jacobson
June 25, 2010
In a recent project, we were minimizing an energy over a surface approximated by a triangle mesh. Our finite element method approach reduced our energy to solving a system of linear equations with coefficients from a stiffness matrix and mass matrix. In the lumped version of a mesh's mass matrix, diagonal entries correspond to areas on the surface around each vertex. You want all the areas to sum to the total area of the surface and you would like the area for each vertex to some how reflect the influence of its incident triangles.
Barycentric
One natural choice is a barycentric area. Take the barycenter (centroid, center of mass), which lies at the intersection of medians. Using those medians divide the triangle into three quadrilaterals each corresponding its incident point:
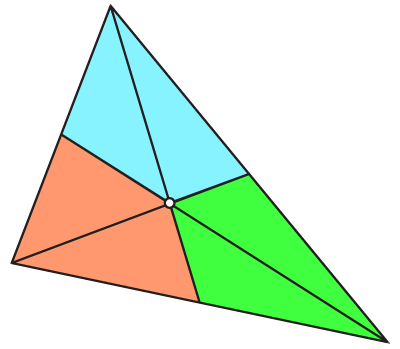These quadrilaterals are by definition of equal area. The barycentric mass matrix entry for vertex i is the sum of its corresponding quadrilaterals from all incident triangles, or more simply: one-third of the total area of all neighboring triangles. Notice that the contribution of a triangle to its vertices is the same for all three, regardless of there placement around the triangle.
Voronoi
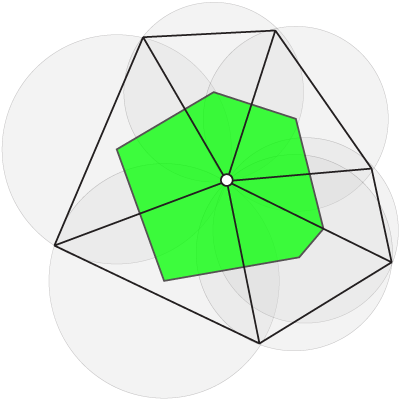
Another, also natural, choice is voronoi area. Take the circumcenter, which lies at the center of the circumscribing circle of the triangle. It follows quickly that the circumcenter is equidistant from all vertices on the triangle. Connect this point to the midpoints along the edges of the triangle, again forming three quadrilaterals.
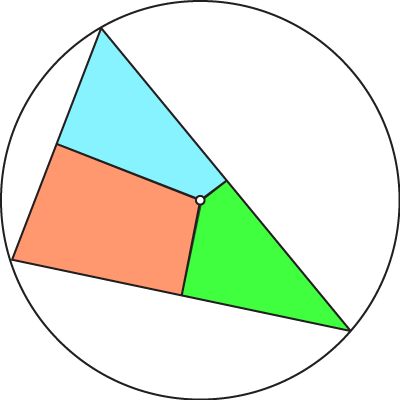Note that this time the quadrilaterals are not equal. They are not even guaranteed to be positive. For obtuse triangles, the acute angled vertices will receive negative areas (assuming you demand their sums equal the area of the triangle). Here is a plot of voronoi areas as the angle of an isosceles triangle grows from 0 (acute) to π (obtuse). The x axis is the angle of the isosceles triangle and the y axis is area. The green line shows the area of corresponding to the vertex at the angle that's growing, the blue corresponds to the other two areas.
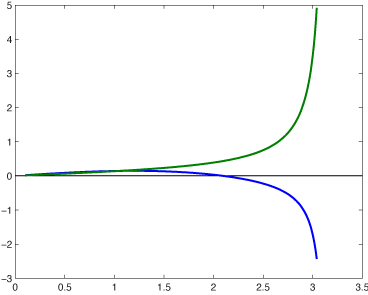Notice that at π/2 we might expect the other two areas to cross into negative but actually this happens later. So voronoi areas won't produce negative coefficients until fairly obtuse.
Again, the voronoi mass matrix entry for vertex i is the sum of its corresponding quadrilaterals from all incident triangles. Since areas can be negative, this means negative entries could end up in the voronoi mass matrix.
Connectivity dependence
The Voronoi area of a vertex is called so because the area represents its corresponding voronoi region: all the points on the surface for which this vertex is the closest vertex (assuming the mesh has "nice" triangles: non-obtuse). In this way the voronoi area depends only on the vertices positioning on the surface not the connectivity of the mesh.
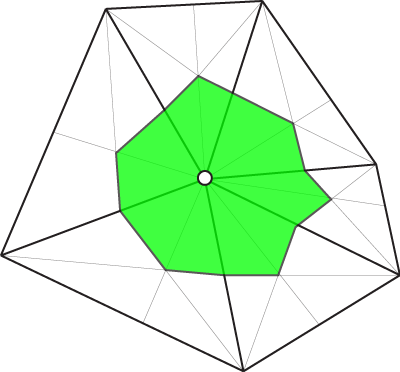
The barycentric area, while having the advantage of always being positive, is heavily connectivity dependent as a vertex gets one-third of the area of any connected triangle.
For a simple example, here're two meshes. One with regular positions and regular connectivity:
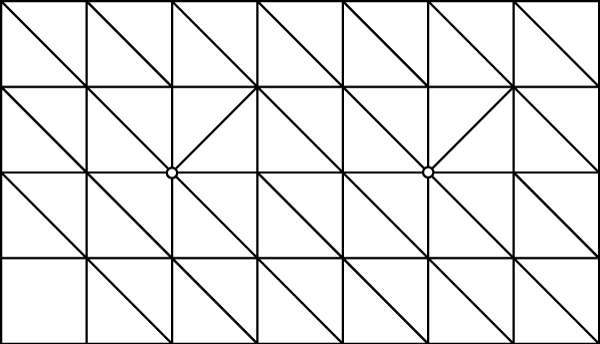
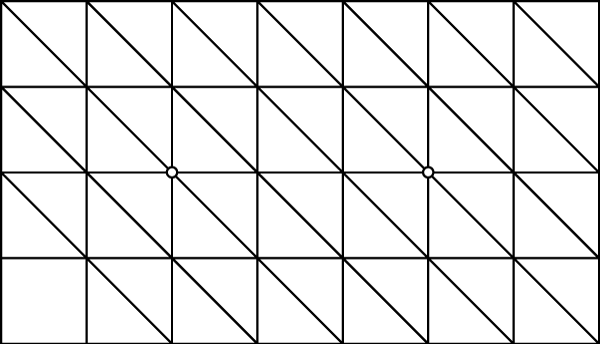And one with regular positions and the same regular connectivity but a single edge at each highlighted vertex has been flipped:
And here are the barycentric (left) and voronoi (right) areas for the highlighted vertices on the regular connectivity mesh.
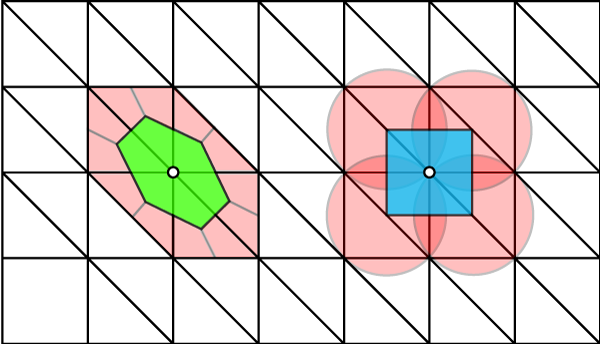Now, notice how when the edge is flipped the barycentric area changes drastically, and actually changes for all vertices incident on the flipped edge. The voronoi however stays the same for this vertex and all vertices.
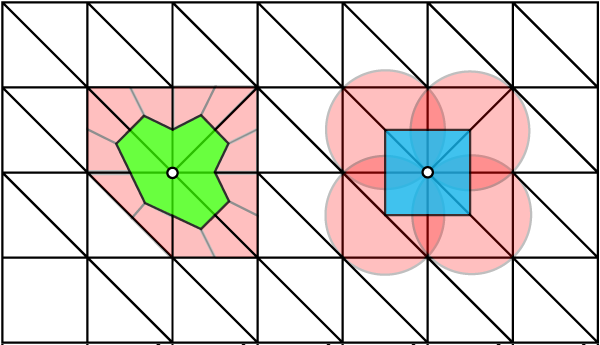
Hybrid approach to vonoroi
To handle the problem of negative voronoi areas for some obtuse triangles, there exists a hybrid approach. For acute triangles, use voronoi as is. For obtuse triangles snap the circumcenter to the midpoint along the edge opposite the large angle and use the corresponding quads (I described this in an earlier post). Notice for a right angle triangle the circumcenter corresponds with this midpoint, so as a triangle becomes obtuse there isn't a jump in area distribution. A keen eye will notice that I am doing this in the voronoi area picture above for the obtuse triangle.