Generate "regular" tetrahedral mesh in MATLAB

Alec Jacobson

December 13, 2010

weblog/

Here is a simple function which generates "regular" tetrahedral meshes in MATLAB. I put regular in quotes because while the positions of the vertices are indeed those of a regular 3D grid, the connectivity is random. This is the result of not connecting the tets myself, instead I just feed the vertex positions to delaunayn, a MATLAB function which constructs the 3D delaunay mesh from a set of points. Perhaps later I will regularize the connectivity... especially because of how slow delaunayn is. Save this in regular_tetrahedral_mesh.m:

function [T,V] = regular_tetrahedral_mesh(nx,ny,nz)
  % REGULAR_TETRAHEDRAL_MESH
  %
  % [T,V] = regular_tetrahedral_mesh(nx,ny,nz)
  %
  % Generates a "regular" tetrahedral mesh with dimensions (nx,ny,nz)
  %
  % Input:
  %   nx  number of points in x direction on grid
  %   ny  number of points in y direction on grid
  %   nz  number of points in z direction on grid
  % Output:
  %   T  tetrahedra list of indices into V
  %   V  list of vertex coordinates in 3D
  %
  % Example
  %    [T,V] = regular_tetrahedral_mesh(3,3,3);
  %    tetramesh(T,V); %also try tetramesh(T,V,'FaceAlpha',0);
  % 
  % See also delaunayn, tetramesh
  %

  % Create a grid
  [x,y,z] = meshgrid(linspace(0,1,nx),linspace(0,1,ny),linspace(0,1,nz));
  V = [x(:) y(:) z(:)];
  if(nx==2 && ny==2 && nz==2)
    warning(['delaunayn vomits on 2x2x2...' ...
      'adding center point at [0.5,0.5,0.5].']);
    V = [V;0.5,0.5,0.5];
  end
  T = delaunayn(V);
end

Then you can call it like this:

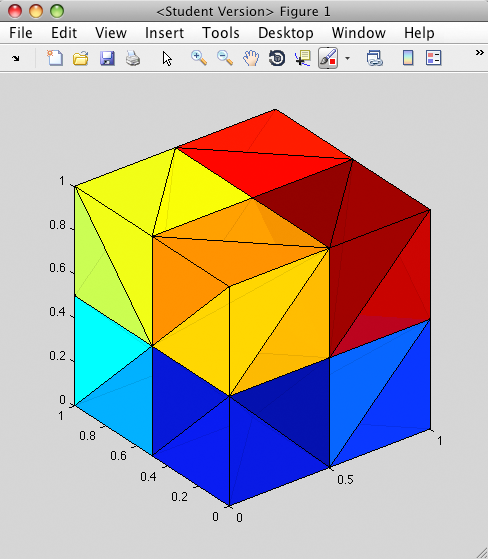
[T,V] = regular_tetrahedral_mesh(3,3,3);
tetramesh(T,V);

which should produce this:

Update: Here's the real regular tetrahedral mesh generator. Complete with regular connectivity. Next step is to keep track of surface faces...


function [T,V] = regular_tetrahedral_mesh(nx,ny,nz)
  % REGULAR_TETRAHEDRAL_MESH
  %
  % [T,V] = regular_tetrahedral_mesh(nx,ny,nz)
  %
  % Generates a regular tetrahedral mesh with dimensions (nx,ny,nz)
  %
  % Input:
  %   nx  number of points in x direction on grid
  %   ny  number of points in y direction on grid
  %   nz  number of points in z direction on grid
  % Output:
  %   T  tetrahedra list of indices into V
  %   V  list of vertex coordinates in 3D
  %
  % Example
  %    [T,V] = regular_tetrahedral_mesh(3,3,3);
  %    tetramesh(T,V); %also try tetramesh(T,V,'FaceAlpha',0);
  % 
  % See also delaunayn, tetramesh
  %

  % Create a grid
  [x,y,z] = meshgrid(linspace(0,1,nx),linspace(0,1,ny),linspace(0,1,nz));
  V = [x(:) y(:) z(:)];
  % meshgrid flips x and y ordering
  idx = reshape(1:prod([ny,nx,nz]),[ny,nx,nz]);
  v1 = idx(1:end-1,1:end-1,1:end-1);v1=v1(:);
  v2 = idx(1:end-1,2:end,1:end-1);v2=v2(:);
  v3 = idx(2:end,1:end-1,1:end-1);v3=v3(:);
  v4 = idx(2:end,2:end,1:end-1);v4=v4(:);
  v5 = idx(1:end-1,1:end-1,2:end);v5=v5(:);
  v6 = idx(1:end-1,2:end,2:end);v6=v6(:);
  v7 = idx(2:end,1:end-1,2:end);v7=v7(:);
  v8 = idx(2:end,2:end,2:end);v8=v8(:);
  T = [ ...
    v1  v3  v8  v7; ...
    v1  v8  v5  v7; ...
    v1  v3  v4  v8; ...
    v1  v4  v2  v8; ...
    v1  v6  v5  v8; ...
    v1  v2  v6  v8];
end

By the way, for a 20 by 20 by 20 grid the updated code is about 200 times faster than the code which calls delaunayn. For bigger grids it will only get better as connecting the tets procedurally is linear and vectorized and delaunayn uses QHull which is in general O(n*log(n)) and I'm not sure how parallelized it is. I generate this 10 by 10 by 10 tet mesh in around a hundredth of a second (rendering it with tetramesh took about 4 seconds )