Barycentric coordinates and point-triangle queries
Alec Jacobson
February 04, 2011
Recently I needed to test whether a bunch of points where on a given triangle in 3D. There are many ways of querying for this, but I found one that was for me both intuitive and convenient. The method uses barycentric coordinates.
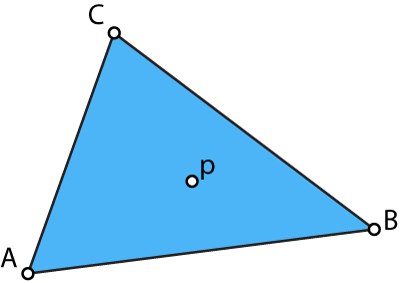
Given a triangle made up of points A, B, and C you can describe any point, p, inside the triangle as a linear combination of A, B, and C: p = λa*A + λb*B + λc*C. That is to say, p can be reproduced as a weighted average of A, B and C. Where the λs are the weights.
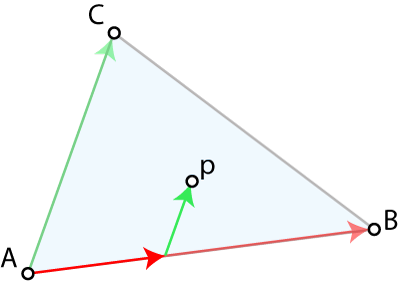
One way to realize this is true is to notice that a triangle can be defined by two vectors, say A→B and A→C, and as long as these two vectors are not parallel we know from Linear Algebra that we can span the whole plane that they define (including the triangle A, B,C which lies on that plane).
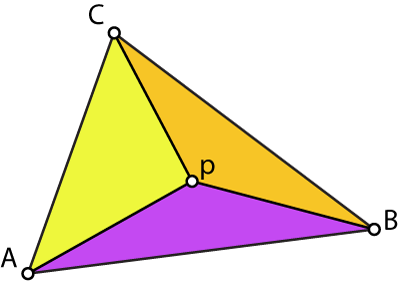
(λa,λb,λc) are called the "barycentric coordinates" of p. Another (more or less unused) name for these are the "area coordinates" of p. This is because λa, λb, and λc are very conveniently defined as:
λa = area(B,C,P)/area(A,B,C)
λb = area(C,A,P)/area(A,B,C)
λc = area(A,B,P)/area(A,B,C)
An important quality of barycentric coordinates is that they partition unity, that is: λa+λb+λc = 1. To see this is true, notice that these sub triangles exactly cover the area of the whole triangle and since we divide be that whole triangle's area we are normalizing the sub triangle areas such that they must sum to one: the barycentric coordinates are the percentages of the area covered by the sub triangles and the whole triangle area. Each sub triangle corresponds to the original triangle corner that is not a corner of the sub triangle. Thus, A corresponds to the sub triangle B, C, p and so forth.
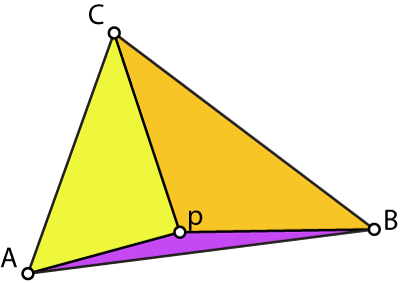
As we move p inside the triangle, ABC, the barycentric coordinates shift. Notice that all coordinates are positive as long as p is inside the triangle.
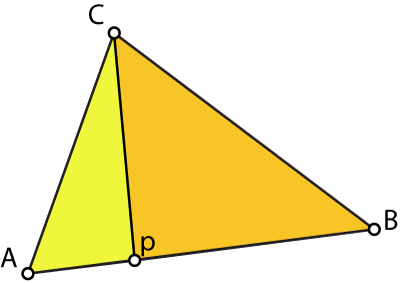
If we move p onto an edge of the triangle then the area of the sub triangle corresponding to the corner opposite that edge becomes zero, thus the barycentric coordinate for p corresponding to that corner is zero.
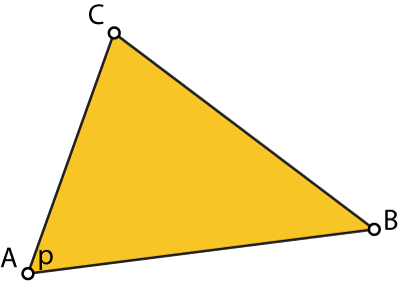
If we move p onto a corner of the triangle then the sub triangle corresponding to that corner is the same (and thus has the as area) as the original triangle, so its corresponding barycentric coordinate to p is 1, the other areas and coordinates being 0.
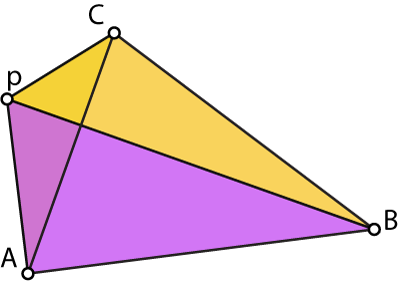
If we move p outside of the triangle the total area covered by the sub triangles will be greater than the original triangle. This is easy to see as the sub triangles always cover the original triangle. We could use this to test whether p is inside the triangle ABC, but there actually a more elegant way that will be handy later.
If instead of computing regular (non-negative) area, we compute signed area then even when we move p outside of ABC the areas will sum to the original area of the triangle ABC. One way to think of signed area is by looking at the orientation of the triangles. Start with p inside ABC.
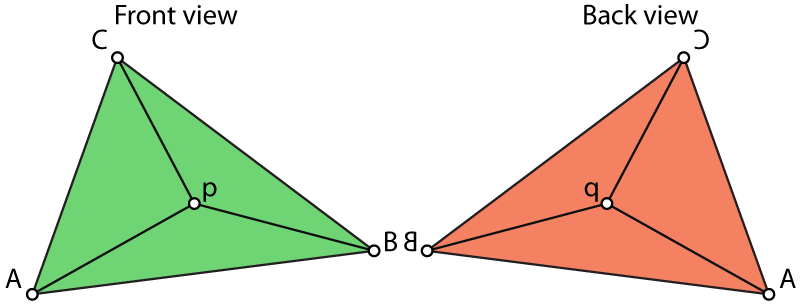
Imagine coloring the side of each triangle facing you green and the back side red. When we move p the triangles change shape, but as long as p stays inside the triangle we still see the same, green side.
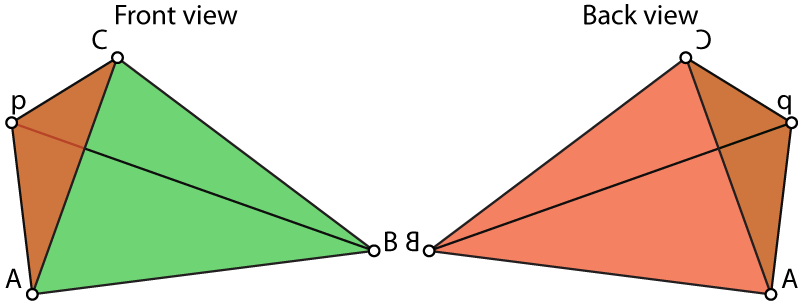
When we pull p outside the triangle the triangle on the edge we crossed gets flipped, and now we see the back, red, side. Now we declare that if we can see the green side of the triangle, its area is positive and if we see the red side of the triangle its area is negative. Now, finally notice that the red side of the flipped triangle when p is outside ABC is always covered exactly by the other two, green triangles. Thus the negative area is cancelled out and we are only left with exactly the original ABC area.
So if we use signed area to compute barycentric coordinates of p, we can determine if p is inside, on, or outside a triangle by looking to see if all coordinates are positive, if any are 0 or if any are negative.
If our triangle is on the 2D plane then this sums up everything we might want to know about p and a given triangle ABC. But if ABC is an arbitrary triangle in 3D and p is also an arbitrary point, then we may also want to know if p whether p is on the plane of the triangle ABC, or if it is above or below the triangle.
We showed above that if p is on the plane of the triangle then the total un-signed area of the sub triangles is greater than the original triangle area and the total signed area of the sub triangles is always exactly equal to the area of the original triangle.
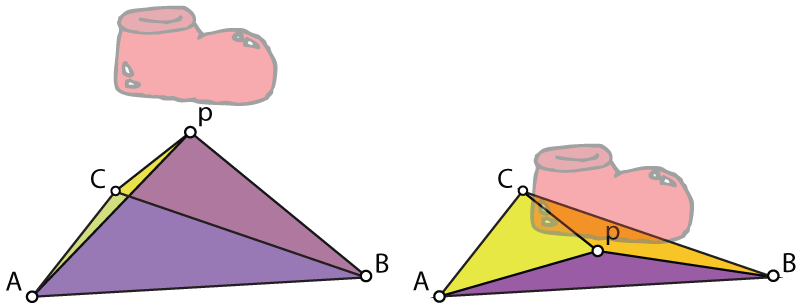
However, if we pull p off the plane of the sum of the total un-signed area of the sub triangles will necessarily be greater than the area of the original triangle. To see this notice that by pulling p off the triangle we are making a tetrahedron pABC with a certain amount of volume, where before pABC was flattened onto the base triangle ABC with no volume. Where ever p is in space it makes such a tetrahedron with ABC and we can always flatten (project) it to the plane of the triangle where we know the total area of the flattened triangles must cover (be greater than) the original triangle ABC. Now finally notice that "flattening" a triangle can never increase the triangle's area (imagine holding a paper triangle in front of your face, your eyes project it onto the plane which you see. There's no way of rotating the triangle so that the projected area (the area you see) is bigger than the actual area of the triangle)).
Finally, we just showed that pulling p away from the plane of the triangle increases the magnitude of each of the sub triangles' area. We may also use this fact to see that the total signed area of these sub triangles is only ever equal to the area of the original triangle if we keep p on the triangle's plane. If we pull p above the triangle (off its front side) then the total signed area is always greater than the original area, and if we pull p below the triangle (off its back side) then the total signed area is always less than the original area. This is harder to see and hopefully I will find a nice way of explaining it.
It's important to note that the areas we get when we pull p off of the plane of the triangle ABC can no longer partition unity, in the sense that if we use these areas as above to define λa, λb, and λc, p will still equal λa*A + λb*B + λc*C, but λa + λb + λc will not equal 1.










