Rotate a point around another point

Alec Jacobson

February 22, 2011

weblog/

Composing rotations and translations is one of the most important operations in computer graphics. One useful application is the ability to compose rotations and translations to rotate a point around another point. rotate around other point Here's how I learned to do this. I find this method the most intuitive.
  1. Translate so that the other point is at the origin
  2. Rotate about the origin by however much you want
  3. Translate back so that the other point is back to its original position
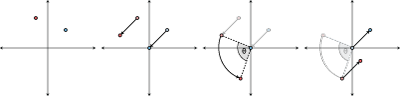rotate around other point This works out nicely with matrix math since rotations around the origin are easily stored as 2x2 matrices: 
                               / cos θ  -sin θ\
Rotation around origin by θ:  |                |
                               \ sin θ   cos θ/
If we call that matrix, R, then we can write the whole operation that rotates a point, a, around another point, b,, as: R*(a-b) + b. Be careful to note the order of operations: (a-b) corresponds to step 1, then left multiply with R to step 2, and finally adding back b is step 3. One convenient fact is that when we look at the transformation as a whole where T(a): a → R*(a-b) + b. Because T is just the composition of rotations and translations it can be decomposed into a single rotation followed by a single translation. Namely, T(a): a → R*(a-b) + b may be re-written as T(a): a → S(a) + t, for some rotation matrix S and some translation vector t. To see this just use the distributive law: R*(a-b) + b = R*a - R*b + b, then S = R and t = R*b + b. 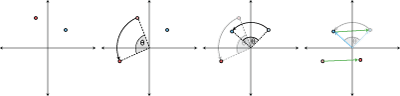So that gives a new derivation of the transformation that rotates a point, a, around another point, b,: R*a - R*b + b. Building an intuition as to why this works is a little tricky. We have just seen how it can be derived using linear algebra but actually seeing this version as each step is elusive. Turns out it helps to make a subtle change. Reverse the last two terms, so that you have: R*a + (b - R*b). Now intuitively we can follow the order of operations and build an intuition:
  1. Rotate first the point about the origin (since the other point is not the origin we've "missed" where we should have been rotated by a certain error amount)
  2. Rotate the other point about the origin by the same amout
  3. Translate by the difference between the original other point and the rotated other point (this is the error amount, because we know that rotating other pointabout itself shouldn't change its position)
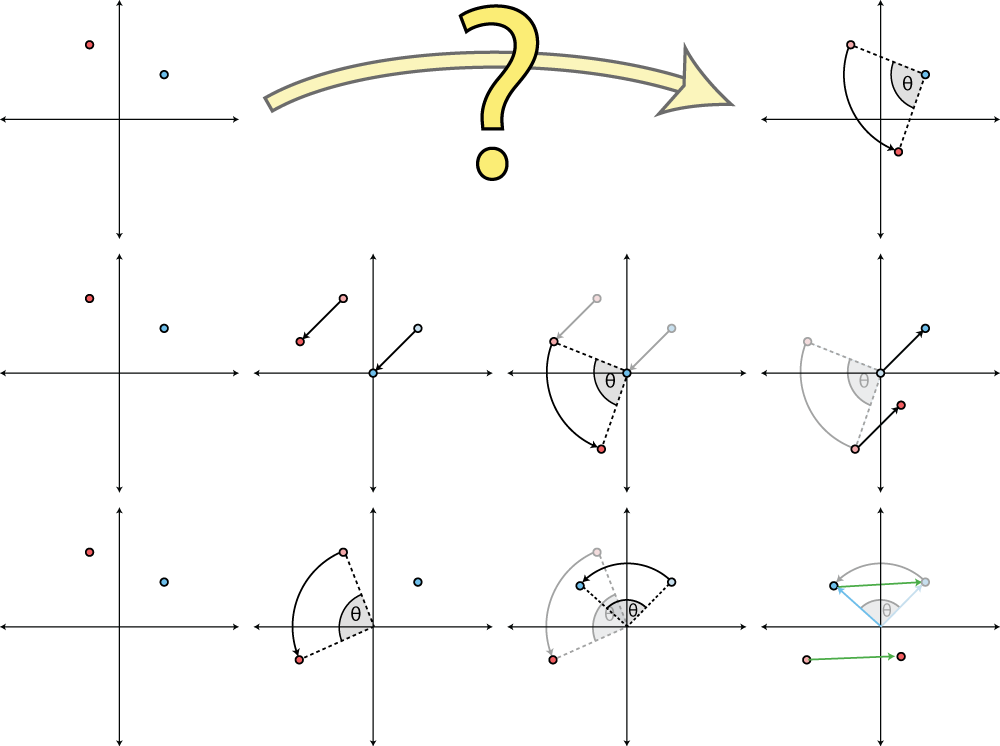
rotate around other point Update: Here's an image comparing these two compositions: rotate around other point