"Element-wise" matrix vector multiplication in matlab

Alec Jacobson

February 23, 2011

weblog/

or

Multiply each matrix in a list of matrices against corresponding vector in list of vectors

Here's a code snippet to take a stacked list of m by n matrices, S, and multiply each m by n matrix by a corresponding n-length row vector in a list of row vectors, V. Resulting in a list of m-length row vectors:

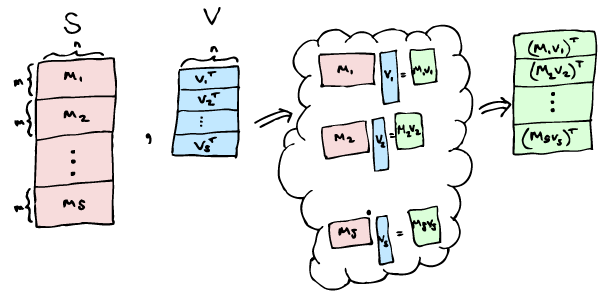multiply each matrix in list against corresponding vector in list

First of all, make your vertical stack of matrices S. So that S(i:(i+m-1),:) = Mi and so forth. And be sure that your list of row vectors is s by n, in V, where s is the number of matrices and vectors. Then you may issue:

I = repmat([1:(m*s)],1,n);
J = repmat(reshape(repmat(1:n:(s*n),m,1),1,s*m),1,n)+reshape(repmat(0:(n-1),s*m,1),1,s*m*n);
SV = reshape(sparse(I,J,S(:))*reshape(V',s*n,1),m,s)';

Often I find that I also have a bunch of matrices stored in a 3d-array, say, T. Where T(:,:,i) = Mi and so forth. I can easily convert T, an m by n by s 3d-array into S, an m*s by n array, using:

S = reshape(permute(T,[2,1,3]),[n,s*m])';

Update: Here's working code that uses the above:

s = 4;
m = 2;
n = 3;
% generate some bogus matrices
S = repmat(eye(m,n),s,1).*repmat(reshape(repmat(1:s,m,1),s*m,1),1,n);
% generate some bogus row vectors
V = reshape(1:s*n,n,s)';
% compute "element-wise" matrix-vector multiplication
I = repmat([1:(m*s)],1,n);
J = repmat(reshape(repmat(1:n:(s*n),m,1),1,s*m),1,n)+reshape(repmat(0:(n-1),s*m,1),1,s*m*n);
SV = reshape(sparse(I,J,S(:))*reshape(V',s*n,1),m,s)';
% view result
SV
% convert vertical stack into 3d array stack
T = permute(reshape(S,[m,s,n]),[1,3,2]);
% convert 3D array stack to vertical stack
TS = reshape(permute(T,[2,1,3]),[n,s*m])';

Update: Here's the for loop version, which is much more straight forward, but starts to slow down in comparison for large s:

SV = zeros(s,m);
for ii = 0:(s-1)
  SV(ii+1,:) = (S((m*ii+1):(m*ii+m),:)*(V(ii+1,:)'))';
end