Re: Suggester shapes
Alec Jacobson
May 08, 2011
Ken recently posted about shapes that suggest math problems. At the end of his post he leaves a riddle:
Find a shape whose area is 1/2 the area of a square and whose perimeter is the same as the perimeter of the square.
Thinking about this riddle a little bit got me thinking about other similar riddles. Like what if I ask the same question but instead of a square use a circle.
Find a shape whose area is 1/2 the area of a circle and whose perimeter is the same as the perimeter of the circle.
My idea for a solution for this new riddle was to intersect to equal-size circles. Notice as long as the circles are equal size if I take the shape that's one of the circles minus the other circle, the perimeter will be the same as a full circle.
So then I just need to find how far apart the circles should be. I know that if the distance between the circles' centers is zero then the left over shape will have area zero. And if the distance is twice their radii then then the left over area will be equal to a full circle. So if I want the left over area to be half the area of a circle I need the distance to be somewhere between zero and twice the radii.
I wrote out the algebra blindly hoping that the equations would collapse leaving me with a beautiful, succinct expression for the necessary distance. The problem turns out to be fairly intangible. Leaving me with a gnarly expression for the distance that is not easily solved. Here's a picture and the expression:
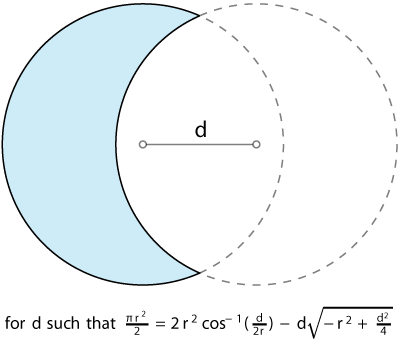
I can approximate d numerically, which reveals d ≈ 0.8079455066. I'm not the first person to try this, this problem also makes an appearance on the Wolfram circle-circle intersection page.
This leaves me wondering if there is a simpler answer to my riddle. Maybe the solution doesn't involve circle-circle intersection at all!
