More useful ease curves

Alec Jacobson

November 16, 2011

weblog/

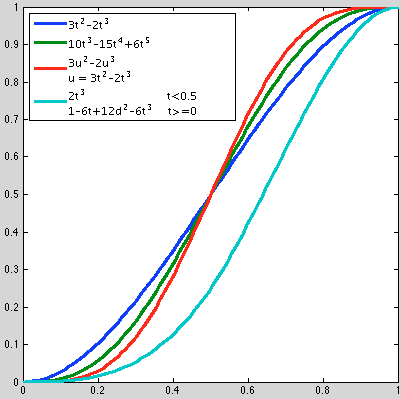
The simplest ease function and the easiest to remember is a cubic:

3*t.^2-2*t.^3

For even better continuity at the corners we could use a fifth order:

10*t.^3 - 15*t.^4 + 6*t.^5

Of course we could always just compose smooth, ease functions to get higher order ones. For example composing the cubic gives:

3*(3*t.^2-2*t.^3).^2-2*(3*t.^2-2*t.^3).^3

So far the ease curves have been symmetric on either side of t=0.5, a useful asymmetric curve is half of a uniform biplane basis function rescaled to fit in the unit square. This one is a piecewise cubic:

2*t.^3                 .* (t<0.5) + ...
(1-6*t+12*t.^2-6*t.^3) .* (t>=0.5)

Notice how I use multiplication against a logical to construct piecewise functions in matlab. To see them in action use:

t = linspace(0,1,100);
plot( ...
  t,3*t.^2-2*t.^3, ...
  t,10*t.^3 - 15*t.^4 + 6*t.^5, ...
  t,3*(3*t.^2-2*t.^3).^2-2*(3*t.^2-2*t.^3).^3, ...
  t,2*t.^3                 .* (t<0.5) + ...
    (1-6*t+12*t.^2-6*t.^3) .* (t>=0.5), ...
  'LineWidth',2 ...
);

third, fifth and ninth order ease curves and half a uniform bspline basis function

The nice legend is created with:

nl = @(s) strrep(s,'\n',char(10));
legend({ ...
  '3t^2-2t^3', ...
  '10t^3-15t^4+6t^5', ...
  nl('3u^2-2u^3\nu = 3t^2-2t^3'), ...
  nl('2t^3                           t<0.5\n1-6t+12d^2-6t^3     t>=0')}, ...
  'FontName','FixedWidth', ...
  'Location','NorthWest', ...
  'FontSize',11);

An earlier post about ease curves