intrinsic cotangent formula

Alec Jacobson

January 23, 2012

weblog/

Here's a derivation of the cotangent of an angle α of a triangle ABC given just the lengths of each side of the triangle.

acute triangle

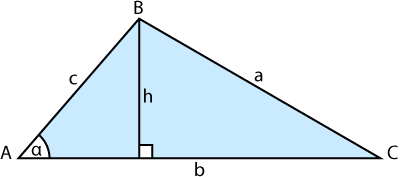
First of all we remind ourselves what cotangent is in terms of cosine and sine: 
        cos α
cot α = ------
        sin α
Now look at cosine and sine separately. By the law of cosines we have that 
a2 = b2 + c2 - 2bc cos α
Rearranging things we have that 
        -a2 + b2 + c2
cos α = ------------
             2bc
Now looking at the sine, we start with the familiar area of the triangle treating b as the base. 
     1
A = --- bh
     2
Using SOH-CAH-TOA, we replace the height: 
     1
A = --- bc sin α
     2
Rearranging this we have: 
         2A
sin α = ----
         bc
Now put the cosine and sine derivations together to get: 
        cos α    -a2 + b2 + c2   bc
cot α = ------ = ------------  ----
        sin α        2bc        2A
Finally arriving at: 
        -a2 + b2 + c2
cot α = ------------
             4A