Visualizing samples on a sphere
Alec Jacobson
May 17, 2013
In my project, I need to uniformly sample directions or equivalently points on the unit sphere. A correct way is to sample the azimuth and cosine of the polar angle uniformly. Another way is to sample points in ℝ3 randomly with mean at the origin and variance 1.
One naive non uniform way, is to sample the x, y and z between [-1,1] uniformly and normalize. I knew that this was biased, but I wanted to see the bias. Here's a small matlab program that continuous splats random points onto a textured sphere:
% Can't use sphere(); have to use funny parameterization so tex-mapping works
n = 100;
theta = (-n:2:n)/n*pi;
sinphi = (-n:2:n)'/n*1;
cosphi = sqrt(1-sinphi.^2); cosphi(1) = 0; cosphi(n+1) = 0;
sintheta = sin(theta); sintheta(1) = 0; sintheta(n+1) = 0;
X = cosphi*cos(theta);
Y = cosphi*sintheta;
Z = sinphi*ones(1,n+1);
% square texture resolution
w = 1000;
im = ones(w,w);
s = surf(X,Y,Z,'FaceColor','texturemap','Cdata',im,'EdgeColor','none');
axis equal;
colormap(gray(255));
method = 'naive';
%method = 'uniform';
%method = 'normal-deviation';
it = 0;
sam = 2000000;
while true
switch method
case 'naive'
% uniformly random 3d point, each coord in [-1,1] and normalize
N = normalizerow(2*rand(sam,3)-1);
case 'normal-deviation'
N = normalizerow(normrnd(zeros(sam,3),1));
case 'uniform'
% random polar angle and azimuth
Z = rand(sam,1)*2-1;
A = rand(sam,1)*2*pi;
R = sqrt(1-Z.^2);
N = [Z R.*cos(A) R.*sin(A)];
end
% project
S = [(N(:,3)+1)/2 (atan2(N(:,2),N(:,1))+pi)/(2*pi)];
% splat!
S = round([mod(w*S(:,2),w-0.5) mod(w*S(:,1),w-0.5)]+1);
im = im + full(1-sparse(S(:,2),S(:,1),1,w,w));
set(s,'CData',matrixnormalize(im));
it = it + 1;
drawnow;
end
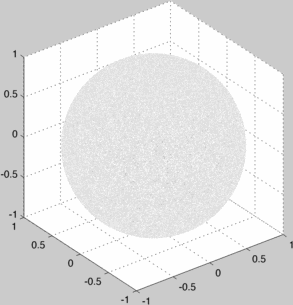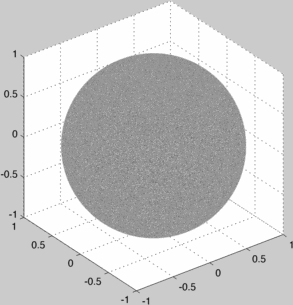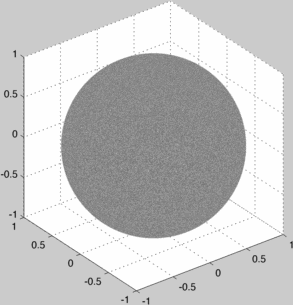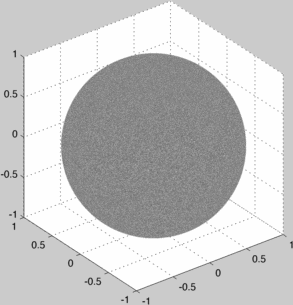
This produces an incrementally improving image of a textured sphere where black means high probability and white means low probability:
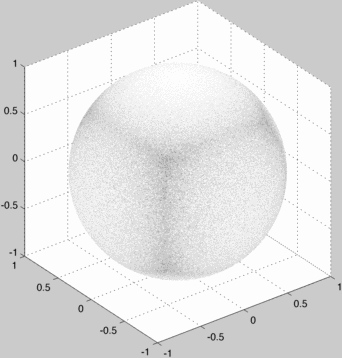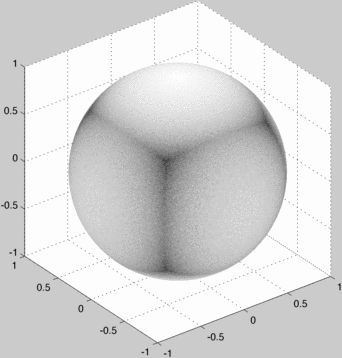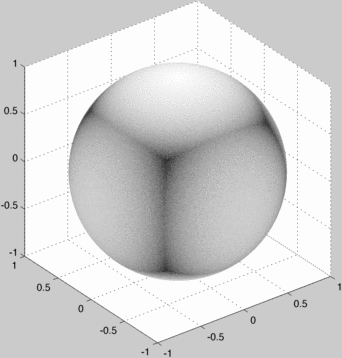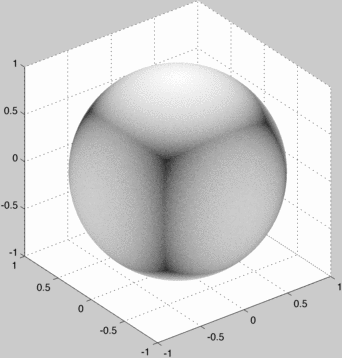
When this converges we can examine the bias around the sphere:
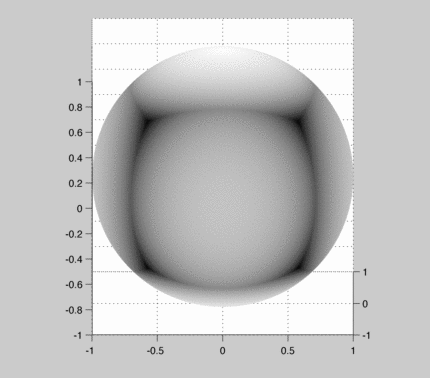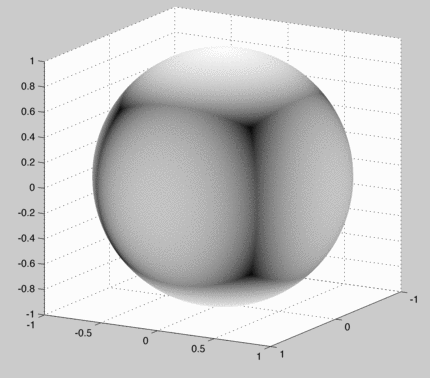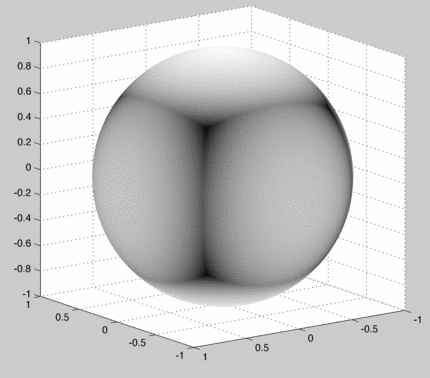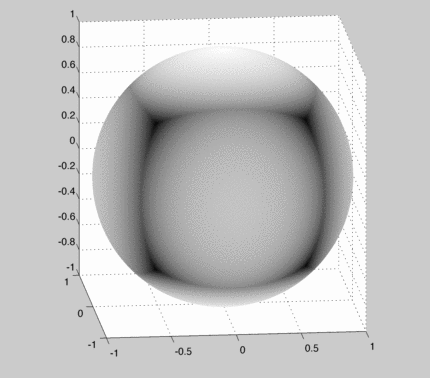
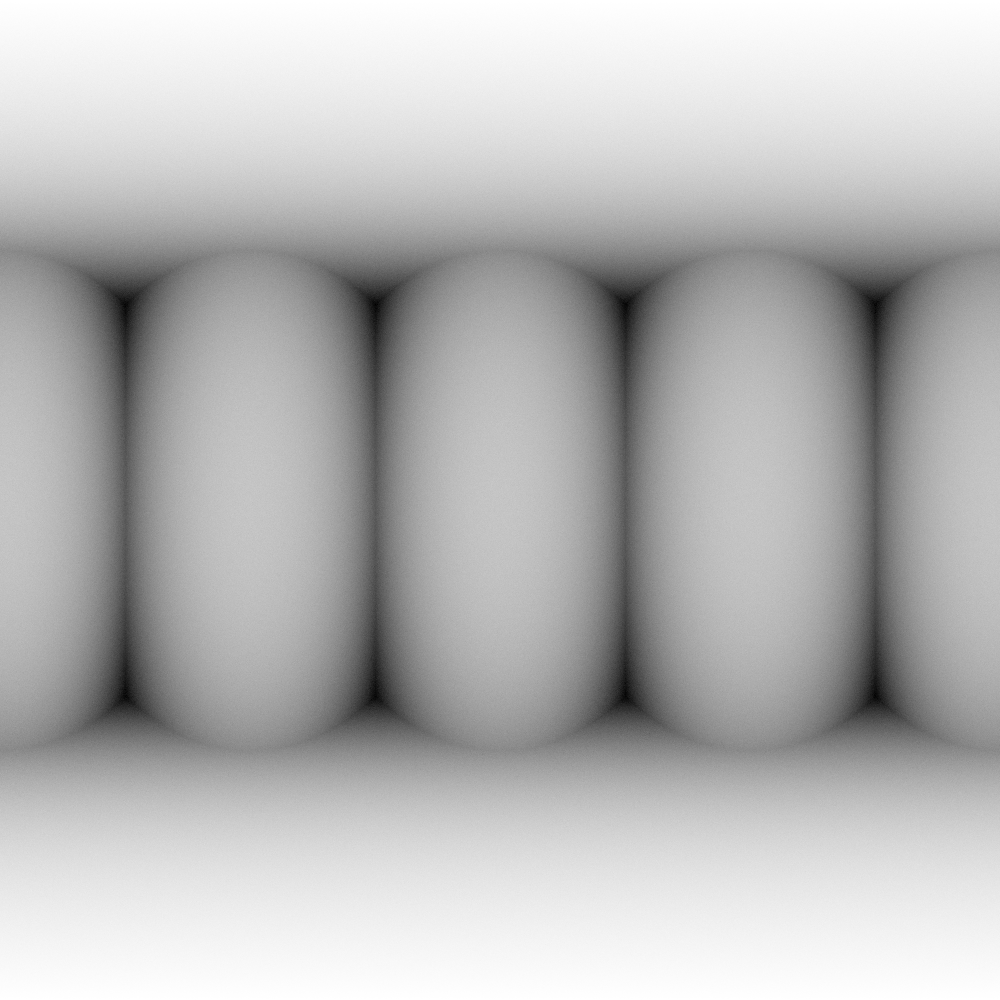
The "converged" texture map looks like:
Of course, a correct uniform sampling converges rather boringly to a uniformly black sphere.
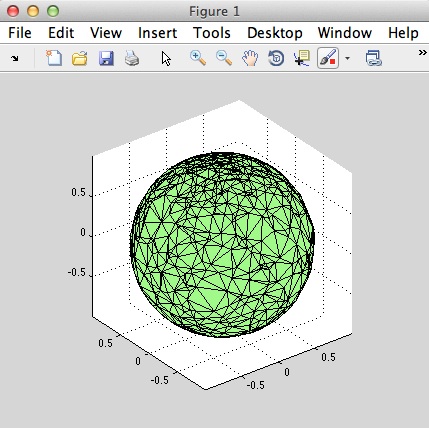
In a different project we need not only a random sampling on the sphere, but also a Delaunay triangle mesh. Since all points lie on the sphere they also lie on their respective convex hull:
V = normalizerow(normrnd(zeros(sam,3),1));
F = convhulln(V);
The result looks something like this: