Smoothly parameterized ease curve
Alec Jacobson
May 23, 2013
Using polynomial ease curves, it's easy to create a function f(x) which obtains f(0) = 0 and f(1) = 1 as well as reaching 0 derivatives f'(0) = 0, f'(1) = 0, f"(0) = 0, f"(1) = 0, etc. One can start with a simple cubic polynomial: f(x) = 3x²-2x³ which achieves first order smoothness (i.e. f'(0) = 0 and f'(1) = 0. Then we can compose this to have higher and higher continuity f(f(x)), f(f(f(x))). This creates a 9th and 27th order polynomials. Here's a sequence of repeated composing this cubic function. The title shows the order: 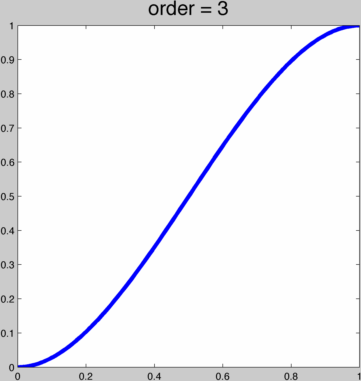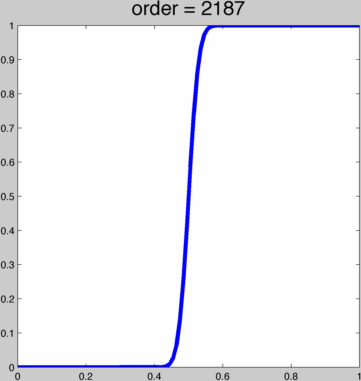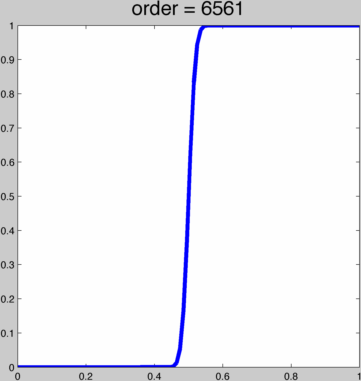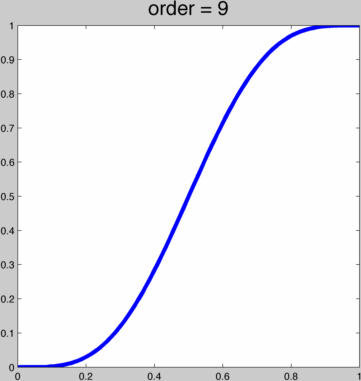 We can also derive such a smooth, symmetric polynomial ease curve for any order 2*k+1, k in ℕ+ polynomial. Thus with k we can have finer, albeit incremental, control over the shape of the function. Here's a ruby script to generate a maple script that will generate the necessary coefficients (there must be a pattern here, but I'm too lazy right now to find it):
We can also derive such a smooth, symmetric polynomial ease curve for any order 2*k+1, k in ℕ+ polynomial. Thus with k we can have finer, albeit incremental, control over the shape of the function. Here's a ruby script to generate a maple script that will generate the necessary coefficients (there must be a pattern here, but I'm too lazy right now to find it):
#!/opt/local/bin/ruby
# Script to generate Maple code for solving for 2*k+1 order polynomial f(x)
# with value f(0) = 0, f(1) = 2 and d<sup>k</sup>f/dx<sup>k</sup>|<sub>0</sub> = 0 d<sup>c</sup>f/dx<sup>c</sup>|<sub>1</sub> = 1, c=1,...,k
smoothness = 3
(1..smoothness).each do |k|
as = (k+1..2*k+1).map{|c| "a#{c}"}.join(",");
puts "f := (#{as},x) -> "
puts " #{(k+1..2*k+1).map{|c| "a#{c}*x^#{c}"}.join("+")};"
puts "solve({"
puts " f(#{as},0)=0,"
puts " f(#{as},1)=1,"
diffs = (1..k).map do |c|
" eval(diff(f(#{as},x),#{(1..c).map{|d| "x"}.join(",")}),x=0)=0,\n"+
" eval(diff(f(#{as},x),#{(1..c).map{|d| "x"}.join(",")}),x=1)=0"
end
puts "#{diffs.join(",\n")}},"
puts " {#{(k+1..2*k+1).map{|c| "a#{c}"}.join(",")}});"
end
Using these coefficients we can plot the first few: 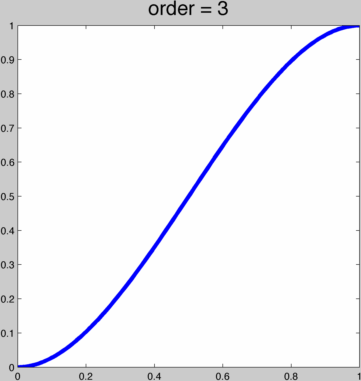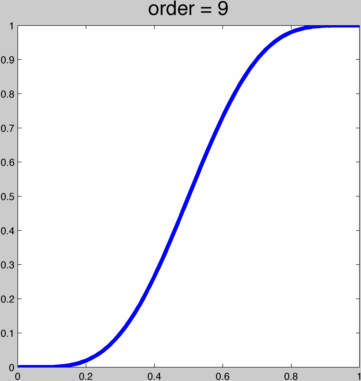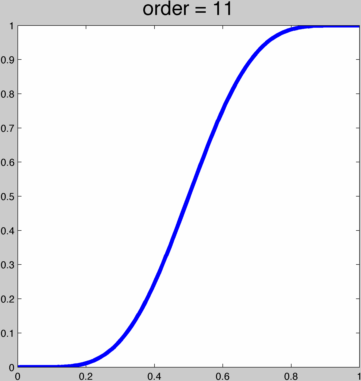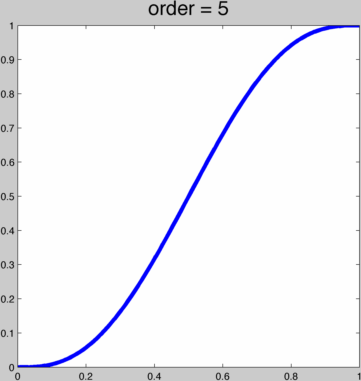 These sequences converge on a scaled and shifted Heaviside step function. But we only have an integer-valued parameter. It'd be nice to have a smooth parameter. If we only cared about this property of the curve getting steeper in the middle as we increase or parameter (while maintaining interpolation and at least C1 continuity, then we could try to do this with a cubic spline. Now we can smoothly increase the steepness, but before reaching the step function the spline curves to far, losing injectivity when treated as a function of x.
These sequences converge on a scaled and shifted Heaviside step function. But we only have an integer-valued parameter. It'd be nice to have a smooth parameter. If we only cared about this property of the curve getting steeper in the middle as we increase or parameter (while maintaining interpolation and at least C1 continuity, then we could try to do this with a cubic spline. Now we can smoothly increase the steepness, but before reaching the step function the spline curves to far, losing injectivity when treated as a function of x. 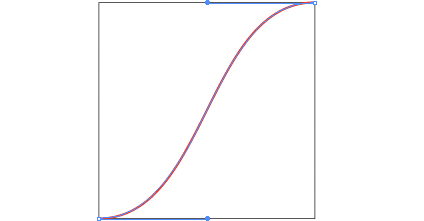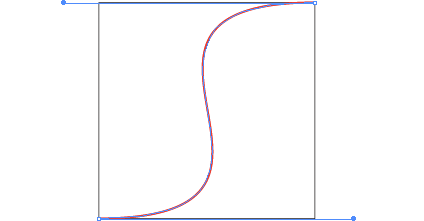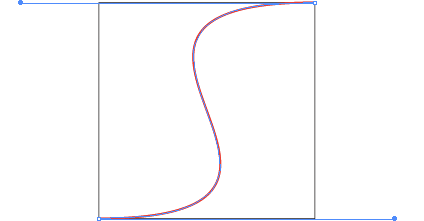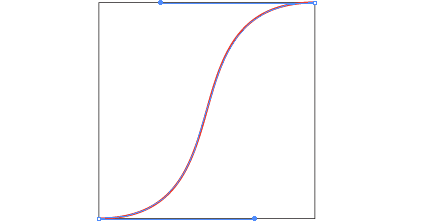 The fact the we cannot reproduce the Heaviside function with a cubic spline should have been obvious anyway. The Heaviside function is loosely a degree ∞ polynomial, with ∞ smoothness at 0 and 1. We can achieve what we want by taking a function which indeed converges to the Heaviside step function: f(x) = 1/(1+e-2tx). We can adapt this to our unit square domain and enforce interpolation for any k: g(x) = (f(2x-1)-1/2)/(f(1)-1/2)/2+1/2, or in MATLAB:
The fact the we cannot reproduce the Heaviside function with a cubic spline should have been obvious anyway. The Heaviside function is loosely a degree ∞ polynomial, with ∞ smoothness at 0 and 1. We can achieve what we want by taking a function which indeed converges to the Heaviside step function: f(x) = 1/(1+e-2tx). We can adapt this to our unit square domain and enforce interpolation for any k: g(x) = (f(2x-1)-1/2)/(f(1)-1/2)/2+1/2, or in MATLAB:
g = @(x,t) (1./(1+exp(-2*t*(2*x-1)))-1/2)/(1./(1+exp(-2*t*1))-1/2)/2+1/2);
This function behaves pretty nicely for t in (0,∞), going from a linear function to the Heaviside step function: 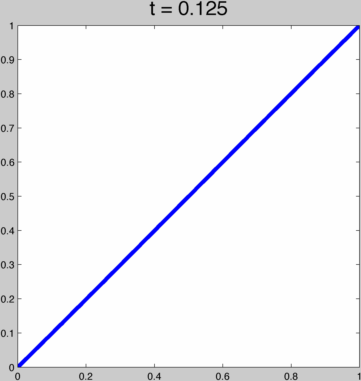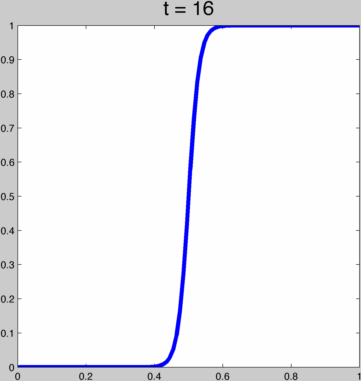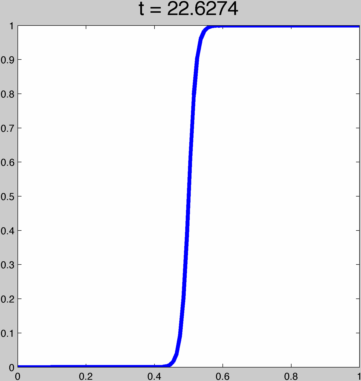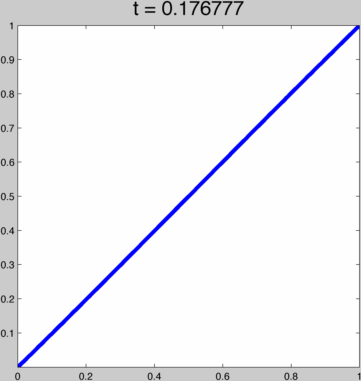 To achieve kth order continuity at our endpoints we can just run this function through (i.e. compose with) one of the 2k+1 order polynomials above. That way, with t we smoothly span a whole space of kth order smooth ease curves. For example, if h(x) = 3x²-2x³ then this is h(g(x)):
To achieve kth order continuity at our endpoints we can just run this function through (i.e. compose with) one of the 2k+1 order polynomials above. That way, with t we smoothly span a whole space of kth order smooth ease curves. For example, if h(x) = 3x²-2x³ then this is h(g(x)): 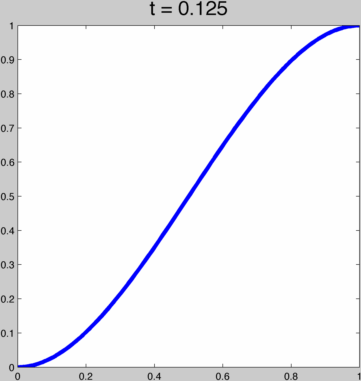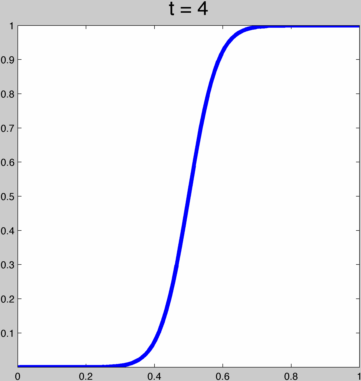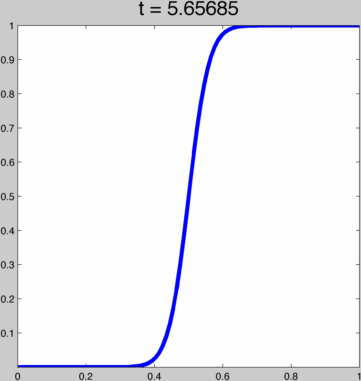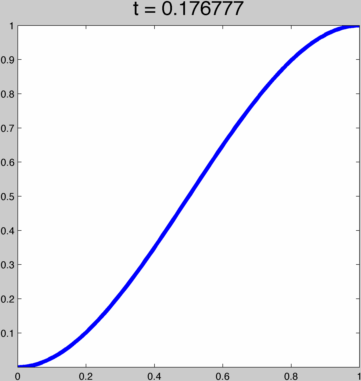
 We can also derive such a smooth, symmetric polynomial ease curve for any order 2*k+1, k in ℕ+ polynomial. Thus with k we can have finer, albeit incremental, control over the shape of the function. Here's a ruby script to generate a maple script that will generate the necessary coefficients (there must be a pattern here, but I'm too lazy right now to find it):
We can also derive such a smooth, symmetric polynomial ease curve for any order 2*k+1, k in ℕ+ polynomial. Thus with k we can have finer, albeit incremental, control over the shape of the function. Here's a ruby script to generate a maple script that will generate the necessary coefficients (there must be a pattern here, but I'm too lazy right now to find it): These sequences converge on a scaled and shifted
These sequences converge on a scaled and shifted  The fact the we cannot reproduce the Heaviside function with a cubic spline should have been obvious anyway. The Heaviside function is loosely a degree ∞ polynomial, with ∞ smoothness at 0 and 1. We can achieve what we want by taking a function which indeed converges to the Heaviside step function: f(x) = 1/(1+e-2tx). We can adapt this to our unit square domain and enforce interpolation for any k: g(x) = (f(2x-1)-1/2)/(f(1)-1/2)/2+1/2, or in MATLAB:
The fact the we cannot reproduce the Heaviside function with a cubic spline should have been obvious anyway. The Heaviside function is loosely a degree ∞ polynomial, with ∞ smoothness at 0 and 1. We can achieve what we want by taking a function which indeed converges to the Heaviside step function: f(x) = 1/(1+e-2tx). We can adapt this to our unit square domain and enforce interpolation for any k: g(x) = (f(2x-1)-1/2)/(f(1)-1/2)/2+1/2, or in MATLAB: To achieve kth order continuity at our endpoints we can just run this function through (i.e. compose with) one of the 2k+1 order polynomials above. That way, with t we smoothly span a whole space of kth order smooth ease curves. For example, if h(x) = 3x²-2x³ then this is h(g(x)):
To achieve kth order continuity at our endpoints we can just run this function through (i.e. compose with) one of the 2k+1 order polynomials above. That way, with t we smoothly span a whole space of kth order smooth ease curves. For example, if h(x) = 3x²-2x³ then this is h(g(x)): 