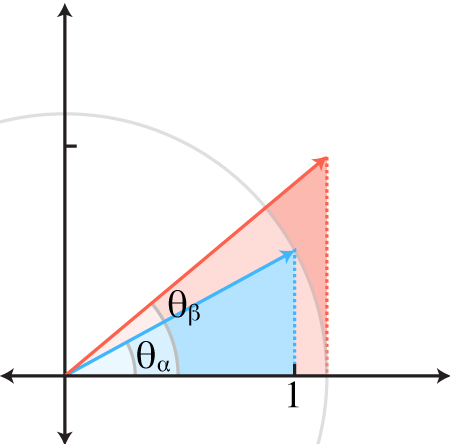
| atan(α) + atan(β) | = atan( (α + β) / (1 - αβ) ) |
| atan(yα/xα) + atan(yβ/xβ) | = |
| θα + θβ | = |
| = θ? | |
| = atan(y?/x?) |

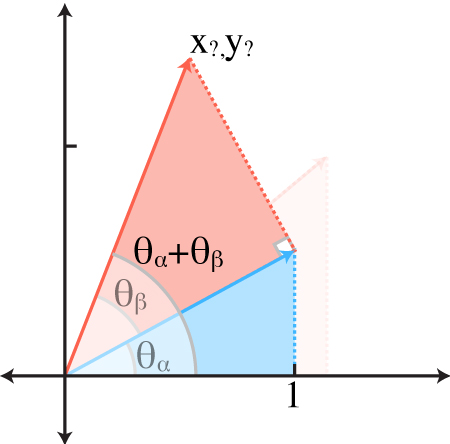
| (x?,y?) = | (xα,yα) + yβ (xα,yα)⟂ / ‖xαyα‖ |
| = | (xα,yα) + yβ (-yα,xα) / ‖xαyα‖ |
| = | (1,yα) + yβ (-yα,1) / xβ |
| y? = | yα + yβ/xβ = α + β |
| x? = | 1 - yβyα/xβ = 1 + α β |