Sparse versus dense Cholesky factorization benchmark

Alec Jacobson

September 18, 2013

weblog/

Here's a very informal benchmark comparing the sparse to the dense Cholesky factorizations as implemented by MATLAB. The problem I'm considering is a Laplace/Poisson equation on an n by n regular grid (x-axis is N = n²). Here's the code I used:

td = [];
ts = [];
N=[];
for n = 1:30
  [V,F] = create_regular_grid(n,n,0,0);
  L = cotmatrix(V,F);
  FL = full(L);
  s = @() chol(-L(2:end,2:end));
  d = @() chol(-FL(2:end,2:end));
  ts = [ts(:);timeit(s,3)];
  td = [td(:);timeit(d)];
  N=[N(:);size(V,1)];
  loglog(N,ts,N,td,'LineWidth',4);
  drawnow;
end

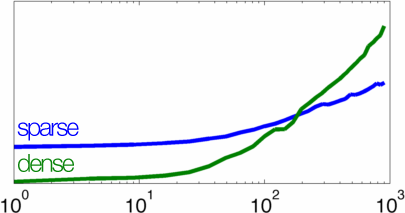
And here is the log-log plot.

sparse vs dense cholesky factorization in matlab benchmark

On my machine, an iMac 3.4 Intel Core i7 with 16GB ram, I see the cross-over point at about N = 200. Shortly after that sparse wins handily.