I wrote a script to compute the ratio of volume inside a given model to the volume of its convex hull. This ratio may be used for various things such as a measure of weak convexity. Here're the average results applied the SHREC target models database.
Ideally I would have a database of solid meshes (closed, self-intersection free). Then I could simply compute the volume inside the shape and divide by the volume of the convex hull. Unfortunately, of the ~720 SHREC models only 91 are closed and of those only 13 are self-intersection free.
So in the absence of a large set of solid meshes, I opted to consider this convex hull volume ratio for closed meshes. Here are the 91 closed meshes in the shrec dataset:

In the presence of self-intersections determining the interior volume is tricky. We could create a conforming Delaunay tessellation of the convex hull, then for each tetrahedron determine if it is inside (say by checking that the winding number is 0). Unfortunately, no truly robust algorithm for conforming delaunay tessellations exists.
Instead, I sampled a regular grid scaled to the bounding box of the shape, throughout those outside the convex hull and then determined which samples were inside the input shape (by checking that winding number is 0).
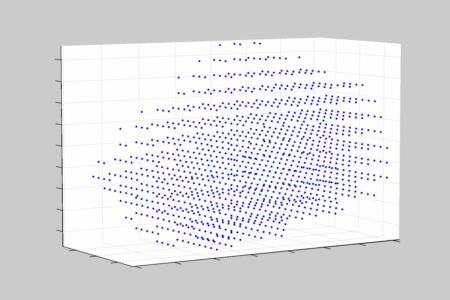
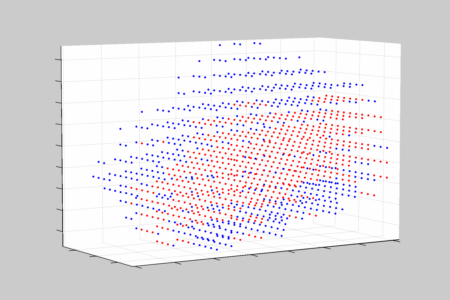
Undoubtedly this will be only an approximation, but given that this input shapes are discrete and finite it should converge as the regular grid resolution increases.
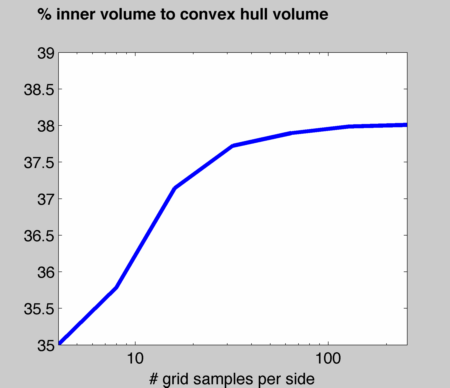
Here's a plot of the average ratio of inner volume to convex hull volume as a function of the number of grid points in a semi-log plot:
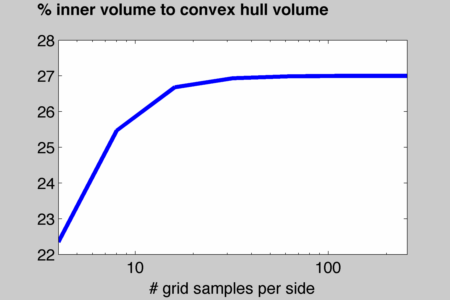
So, for this set of shapes (which spans quite a variety) the ratio is roughly 30%.
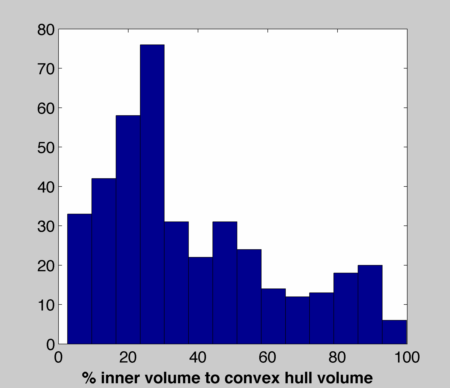
Here's a histogram for the finest resolution I tested (256x256x256 = 16777216 samples):
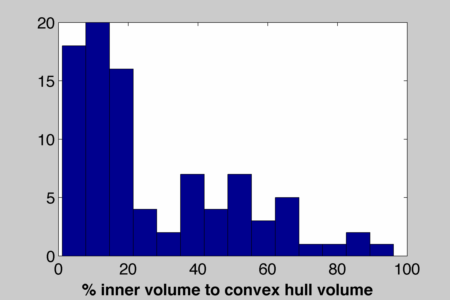
Update: Here're the results from the watertight models in the Princeton Surface Correspondence Benchmark. There the average is more like 38%. Here're the same plots.