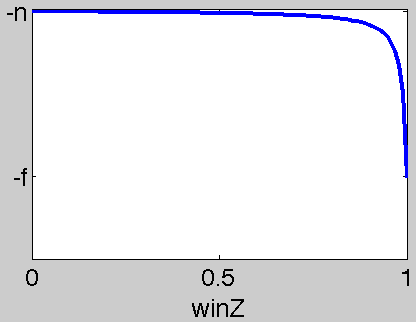
I was trying to unproject a depth image into an OpenGL and was bit surprised to find that my choice of near and far plane values affected the influence of my "window Z" values used to unproject. This really shouldn't have been a surprise when considering how the perspective matrix is formed. If you're using gluPersepctive then your projection matrix P is:
P = / x 0 0 0 \
| 0 y 0 0 |
| 0 0 (f+n)/(n-f) 2fn/(n-f) |
\ 0 0 -1 0 /
where x and y control the field of view angle and aspect ratio, and f and n are the far and near clipping depths respectively.
The projection of a world point z = (0 0 z 1)T is then given by computing p = P * z then applying perspective division q = p / p.w. Despite the incorect documentation, gluProject then computes a window "depth" via winZ = (q.z+1)/2.
Following these formulae we can derive a relationship between winZ and the z-coordinate of our point on the z-axis. Namely,
winZ = (p.z/p.w+1)/2
p.z/p.w = 2*winZ-1
p.w = -z
p.z = z*(f+n)/(n-f) + 2fn/(n-f)
(z(f+n)/(n-f) + 2fn/(n-f))/(-z) = 2winZ-1
z = fn/(f*winZ-n*winZ-f)
or equivalently
winZ = f(n+z)/((f-n)z)
Notably, when z=-f then winZ = 1 and when z=-n then winZ = 0. In between, we have an inverse relationship:
