A very simple method for approximate blue noise sampling on a triangle mesh

Alec Jacobson

October 25, 2014

weblog/

This morning I was looking over the recent methods for generating blue-noise random samples on an arbitrary surface. Many of them involve dart throwing with complicated rejection schemes to achieve a Poisson-disk sampling (e.g. "Feature-preserving direct blue noise sampling for surface meshes" [Peyrot et al. 2014]), some involve hefty optimization procedures (e.g. "Blue Noise through Optimal Transport" [de Goes et al. 12]). A lot of the effort is spent trying to preserve features. I wasn't particularly interested in this at the moment, and I just wanted something simple I could quickly code up and play with.

My idea stemmed from the observation that if my surface is a sphere, and I have a enough samples then the distance between samples will approximate their distance in Euclidean space. So an algorithm for Poisson-disk sampling the sphere looks like:

  1. Generate n uniformly random samples on the sphere
  2. For each sample i find distance dij to closest other sample j, in usual R3 sense
  3. Repeat steps 1 and 2 recursively for all samples i such that i < j and dij < re.

where re is the expected radius between samples on the surface. On the unit sphere, this is easy to compute: something like re = sqrt(4/n).

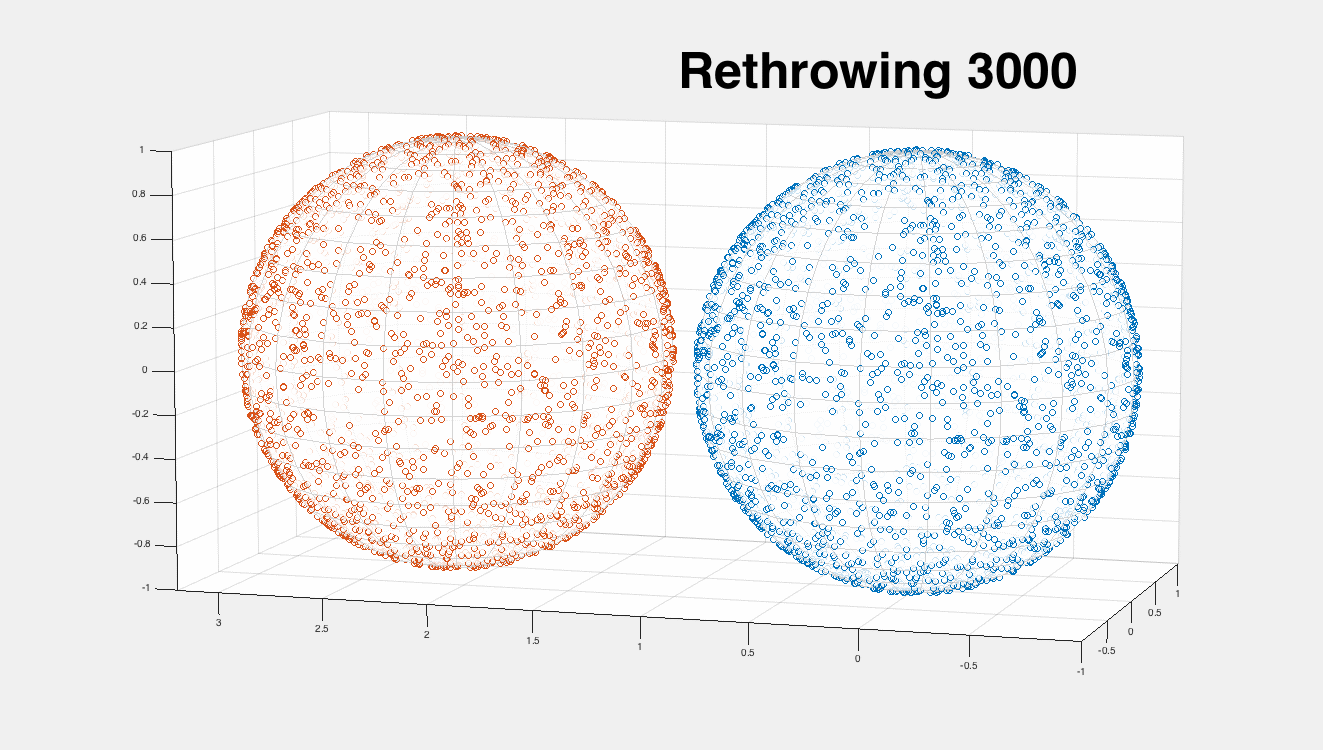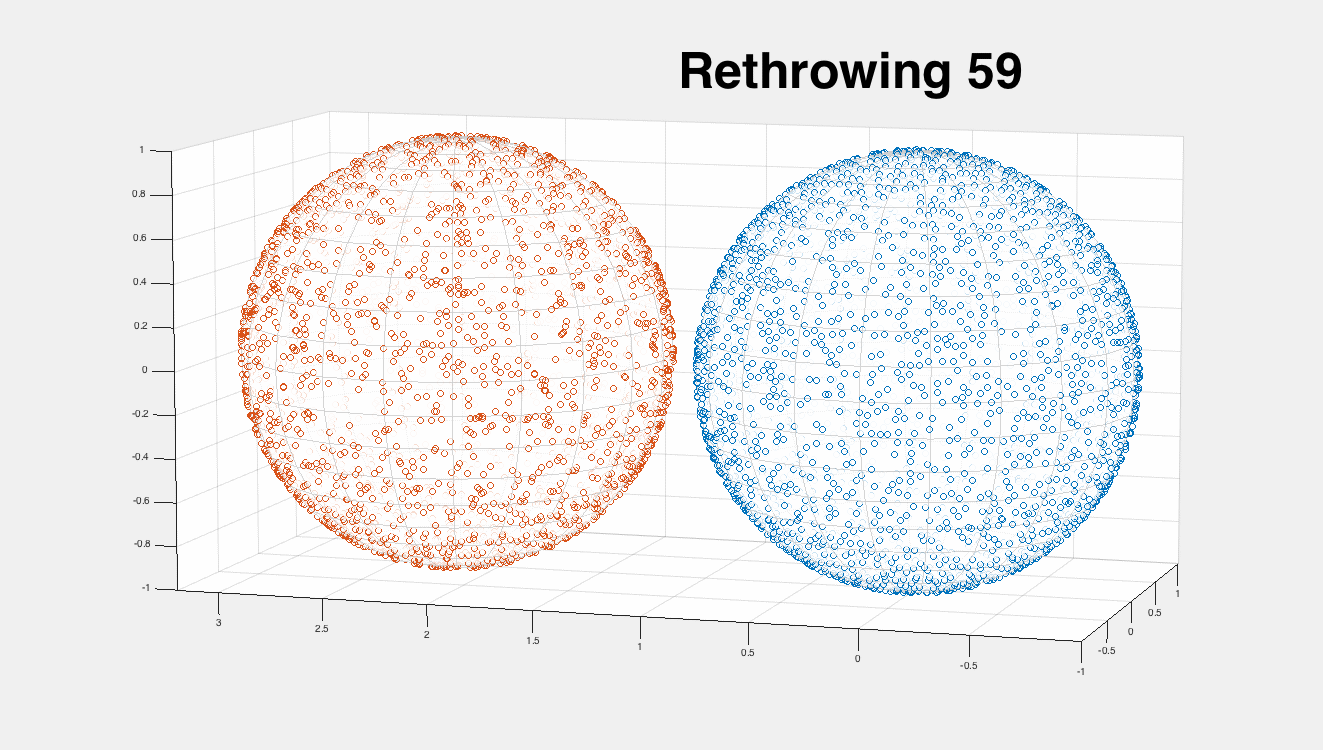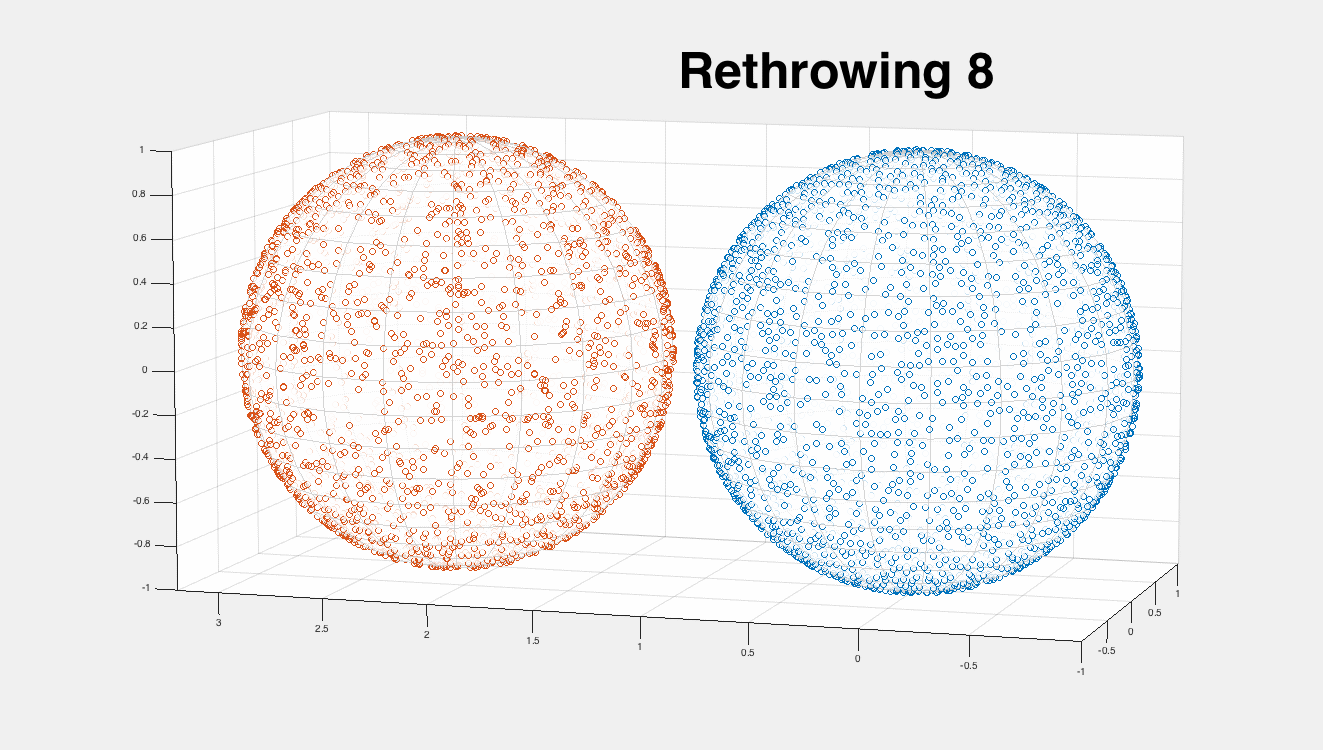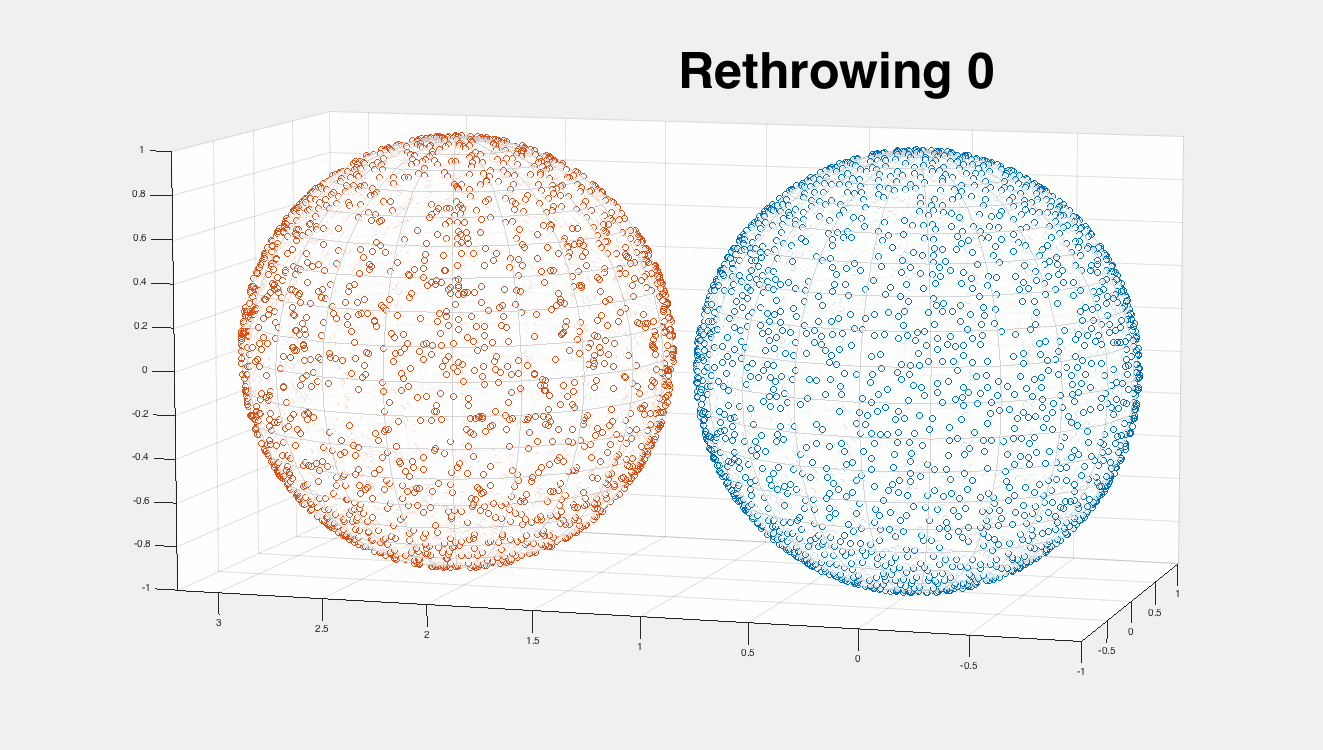
This works quite well:

blue noise sampling on sphere

on the left is the original "white noise" uniform sampling, and on the right I show the iterations of this algorithm converging to a Poisson-disk-like sampling.

Now, for an arbitrary surface my original assumption is no longer true. There may be parts very close to each other in R3 but very far away in terms of the geodesic distance on the surface.

However, there exist a family of methods that lift a surface to an (usually higher dimensional) embedding Rn so that Euclidean distance in Rn approximates geodesic distance (e.g. "Biharmonic Distance" [Lipman et al. 2010]). Using this I can alter my method only slightly to work with arbitrary surfaces:

  1. Lift surface to Rn using "Biharmonic embedding"
  2. Generate n uniformly random samples on the original surface (the one still in R3)
  3. For each sample i find distance dij to closest other sample j, after lifting to Rn
  4. Repeat steps 2 and 3 recursively for all samples i such that i < j and dij < re,

but this time re is not so obviously computed. It would be easy to compute the expected geodesic distance radius, but unfortunately the biharmonic embedding I'm using does not preserve units (i.e. dij is only relative to the geodesic distance between samples i and j on the mesh). I could probably compute the expected distortion during the lift to Rn and derive re from that. But I found it much easier to just take the average closest distance between the original n samples after being lifted to Rn. If I recall correctly, this should converge to the correct expected radius as n goes to infinity. So for large n this should be a reasonable thing to do.

It's working quite well:

blue noise sampling on cheburashka

again, on the left is the original "white noise" uniform sampling, and on the right I show the iterations of this algorithm converging to a Poisson-disk-like sampling.

I've put up matlab code for this in the mesh/random_points_on_mesh.m in my gptoolbox on git. Here's a use example:

[V,F] = load_mesh('/usr/local/igl/libigl/examples/shared/cheburashka.off');
n = 3000;
Pwhite = random_points_on_mesh(V,F,n);
Pblue = random_points_on_mesh(V,F,n,'Color','blue');
t = tsurf([F;size(V,1)+F],[V;V(:,1)+1.1*(max(V(:,1))-min(V(:,1))) V(:,2:3)],'FaceColor','w','EdgeColor','none','FaceAlpha',0.8);
apply_ambient_occlusion(t);
hold on;
scatter3(Pblue(:,1),Pblue(:,2),Pblue(:,3));
scatter3(Pwhite(:,1)+1.1*(max(V(:,1))-min(V(:,1))),Pwhite(:,2),Pwhite(:,3));
hold off;
axis equal;

Note: The current code is rebuilding a k-nearest neighbor acceleration data structure for all samples every iteration. Surely, this could be optimized.