Recently, a student I'm working with installed the SuiteSparse toolbox for matlab and reported wild speedups (20x) over matlab's built-in backslash (\ or mldivide) linear system solver. I thought surely precomputing a cholesky factorization with good ordering (chol with 3 output params) will fair better. But the student was claiming even 5-10x speed ups over that.
Too good to be true? I decided to do a quick benchmark on some common problems I (and others in geometry processing) run into.
I started with solving a Laplace equation over a triangle mesh in 2d. I generated Delaunay triangle meshes of increasing resolution in the unit square. Then I solved the system A x = b in three ways:
\ (mldivide):
x = A\b;
chol + solve:
[L,~,Q] = chol(A,'lower');
x = Q * (L' \ (L \ ( Q' * b)));
cholmod2 (SuiteSparse):
x = cholmod2(A,b);
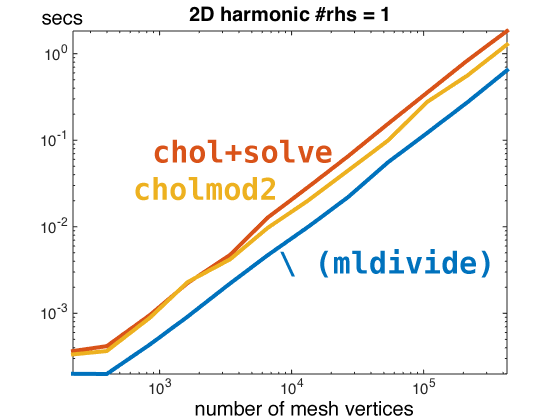
For the Laplace equation with a "single right hand side" (b is a n long column vector), I didn't see any noticeable improvement:

The only thing surprising here is actually how handily backslash is beating the other two.
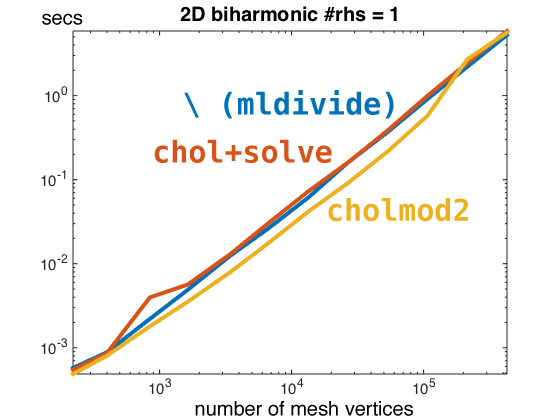
Laplace operators in 2D are very sparse matrices (~7 entries per row). Next I tried solving a bi-Laplace equation which has the sparsity pattern of squaring the Laplace operator (~17 entries per row). Here we see a difference but it doesn't seem to scale well.
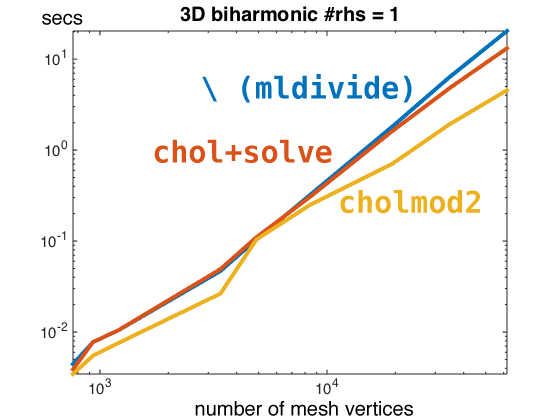
The sparsity patterns of Laplace and bi-Laplace operators are larger in 3d. In particular a nicely meshed unit cube might have upwards of 32 entries per row in its bi-Laplacian. Solving these systems we start to see a clear difference. cholmod2 from SuiteSparse is seeing a 4.7x speed up over \ (mldivide) and a 2.9x speed up over chol+solve. There is even the hint of a difference in slope in this log-log plot suggesting SuiteSparse also has better asymptotic behavior.
So far we're only considering a single right hand side. Matlab's parallelism for multiple right hand sides (during "back substitution") seems pretty pitiful compared to SuiteSparse. By increasing the number of right sides to 100 (b is now n by 100) we see a clear win for SuiteSparse over matlab: 12x speed up over \ (mldivide) and a 8.5x speed up over chol+solve. Here the asymptotic differences are much more obvious.
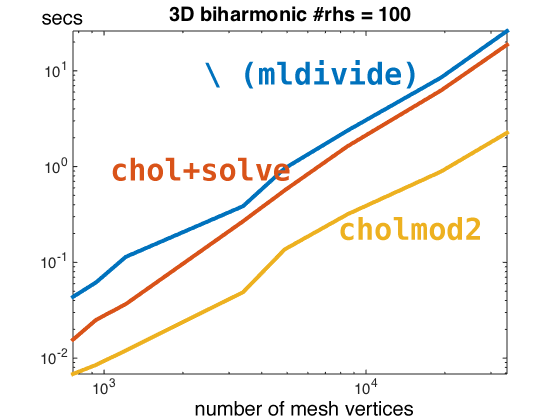
My cursory conclusion is that SuiteSparse is beating matlab for denser sparse matrices and multiple right-hand sides.