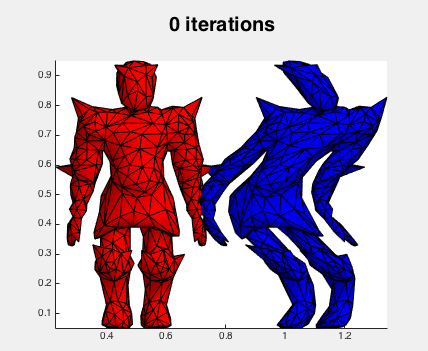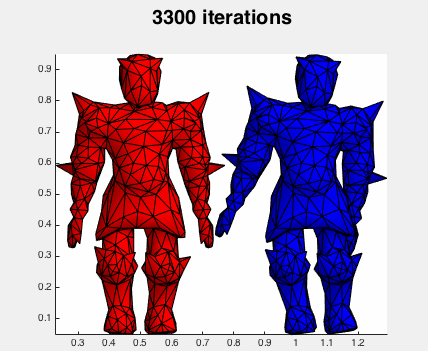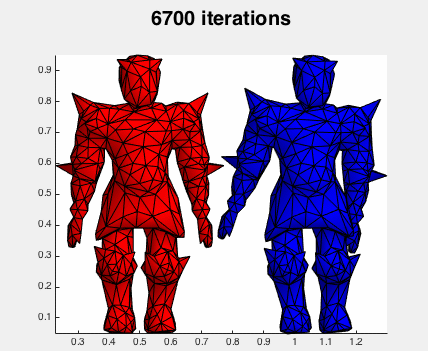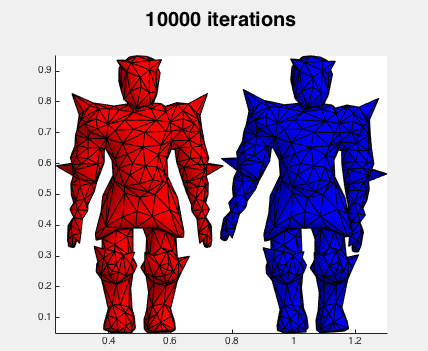
For a long while now I've been curious to implement Newton's method for minimizing as-rigid-as-possible (ARAP) energies. I finally had an excuse to put the pieces together. Find the arap_gradient.m and arap_hessian.m functions in my gptoolbox for matlab.
First, to see what gradient descent looks like:

The red mesh is the original for reference, and the blue begins distorted and is restored via gradient descent. The iterations are simply:
while true
[G,E] = arap_gradient(V,F,U);
U = U - delta_t * G;
end
Convergence is quite slow (I'm displaying every 100 iterations!). I've even increased delta_t as much as I can without hitting instabilities.
In comparison, here's Newton's method:
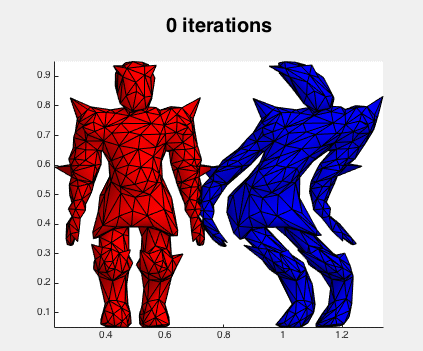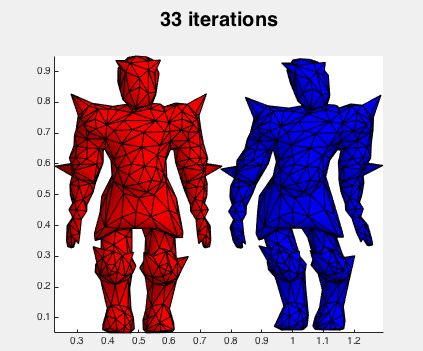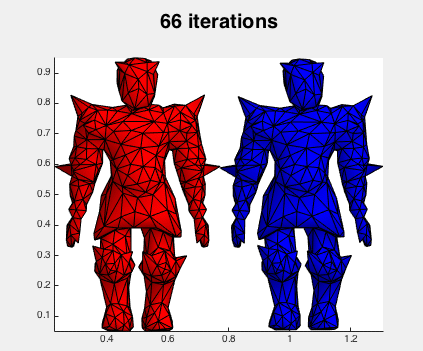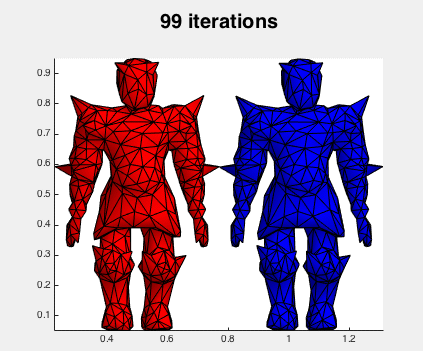
Not surprisingly Newton's method is much faster (done in 100 iterations). Here's what the iterations look like:
while true
[G,E,R] = arap_gradient(V,F,U);
H = arap_hessian(V,F,'EvaluationPoint',U,'Rotations',R);
U = U - delta_t * reshape((H+mu*I) \ G(:),size(U));
end
where mu~=1e-6 is a small number accounting for the instability of the Hessian. I guess this makes it Levenberg-Marquardt, though I'm not updating mu.
For those interested, the paper "A Simple Geometric Model for Elastic Deformations" [Chao et al. 2010] has derivations for both the gradient and Hessian. Though I find their mathematical conventions difficult to parse.
The gradient is straight-forward if you've already implemented the popular "local-global" solver approach. Just conduct your local step (find best fit rotations R) and build (but don't solve) your Poisson equation A X = B. This equation comes from minimizing the ARAP energy with R held fixed: E(X) = 1/2 X' A X - X' B. Now you know that Grad E at X with the best fit R is A*X - B.
The Hessian takes a bit more work. I prefer the derivation in "Shape Decomposition Using Modal Analysis" [Huang et al. 2009]. Besides being mindful of small typo, one must adapt their derivation a bit. They derive the Hessian assuming evaluation at the rest state (where all best fit rotations are identities). To account for this, build the covariance matrices using the evaluation point vertex positions and then left multiply them by the same best fit rotations used when computing the gradient.
Update: A friend also showed me a derivation of the Hessian of the (more or less equivalent) co-rotation elasticity energy in "Material Point Method for Snow Simulation" [Stomakhin et al. 2013]. The procedure looks very well explained though I haven't given it enough time to parse the dense tensor/index notation yet.