Matlab has only rudimentary support for visualizing data defined over a tetrahedral mesh. I use usually external calls to medit. Today I needed to implement slicing through a tet mesh for a different application and noticed that it's also useful for visualization. I add slice_tets.m to gptoolbox. The slicing works in an obvious, yet vectorized way. The way a plane passes through a tet (if at all) can be described by the number of vertices on either side of the plane: 0-4, 1-3, 2-2, 3-1, 4-0. The 0-4 and 4-0 cases don't add anything to the slice and are quickly ignored. The 1-3 and 3-1 cases add a single triangle to the slice and if we categorize the vertices with respect to their signed distance to the plane, then we only need to implement the 1-3 case and reverse the signs to handle the 3-1 case. Finally the 2-2 case adds a quad (i.e. two triangles) to the slice, and we should be careful to flip the orientation depending on which vertices end up on either side.
My vectorized matlab identifies the case each tet belongs to and computes triangles or split quads for all of that case in unison.
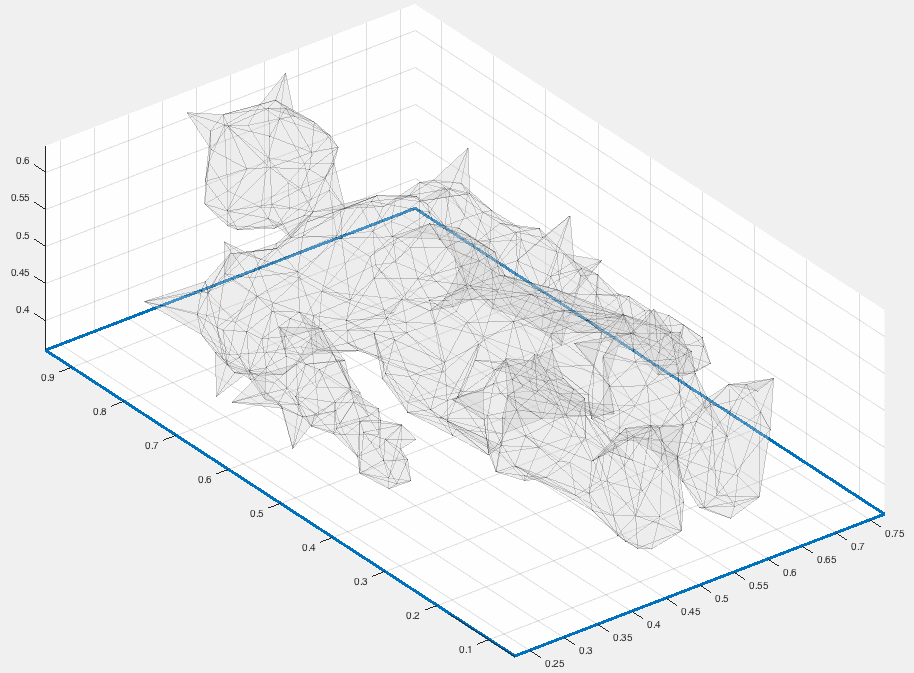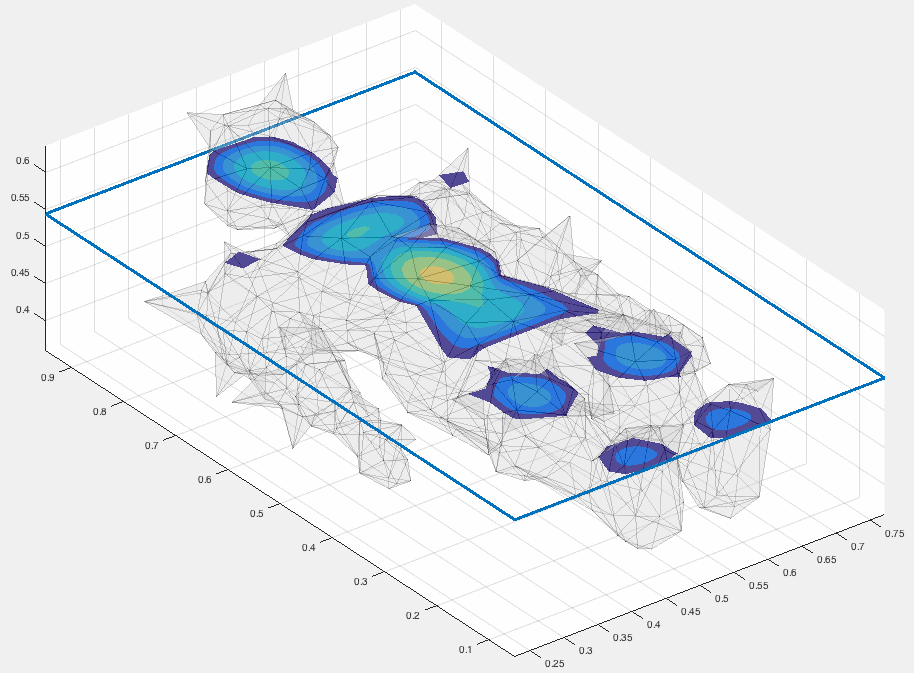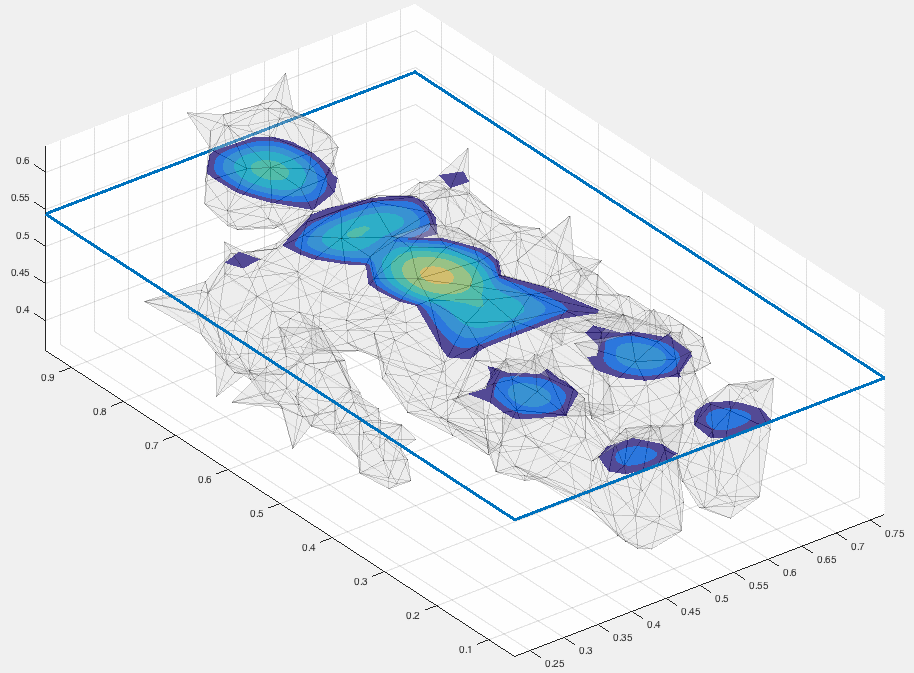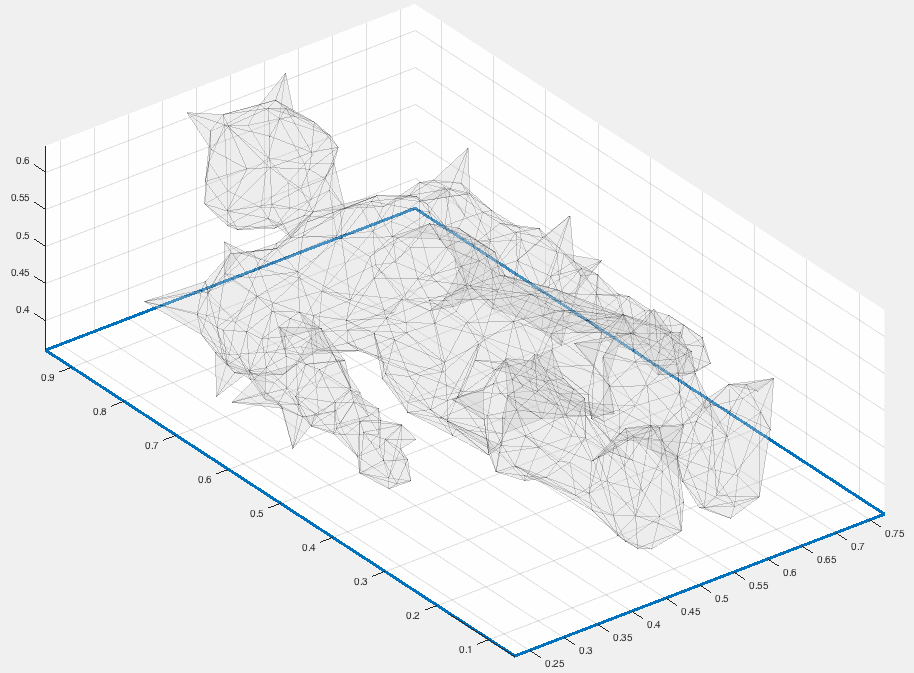
The slicing is actually pretty fast. For a 600,000 tetrahedra mesh, slicing through the middle takes ~0.11 secs (~9fps). With a little more time spent, I may also keep track of the linear interpolation coordinates so that I can visualize a function defined over the tet-mesh onto the slicing plane.
Here I'm showing a slice through a Poisson equation inside this reclining knight: