There's a long chain of work on symmetry detection algorithms for 3d shapes. The mathematics behind a lot of these works is quite interesting and well founded. See "Symmetry in 3D Geometry: Extraction and Applications" [Mitra et al. 2012] for a survey. But for the sake of implementing something quick and dirty with tools I have lying around, here's a solution that largely ignores all this great work.
The workhorse of the solution I arrived at is rigid registration using iterative closest point (aka ICP or Insane Clown Posse). This algorithm is quite simple. To find the best rotation and translations that aligns point set B to point set A:
while not converged
find closest point a* in A to each point b in B
find closest point b* in B to each point a in A
update B with the rigid transform (R,t) best
aligning all pairs a* to b and b* to a
Rigid ICP itself has a wide literature of improvements strategies and optimization alternatives. Besides performance, the main concern is getting stuck in a local minimum. One solution is to consider a variety of initial rigidly transformed seeds for B
Now, if I have a shape A and I take B=A, obviously I'll get back the identity transformation after ICP. If A is rotationally symmetric and I seed B with rotated versions of A. I'll expect that the local minima I find with very low energy will be aligned with symmetry rotations.
But how can I use this to find planes of reflectional symmetry? Well, if I seed B with many rotations of a reflection of A. Then low energy local minima of rigid ICP will reveal reflectional symmetry planes.
A vanilla brute force algorithm might try to sample all reflection planes directly. But this will waste time considering spans of planes far from optimal. Using rigid ICP can be thought of as a way to quickly converge on decent places to look.
My current implementation is a sort of particle swarm optimization. I generate k random seeds for the reflections of A, run rigid ICP on each for j iterations, pick the best i candidates, generate k*f seeds around these candidates, and so on.
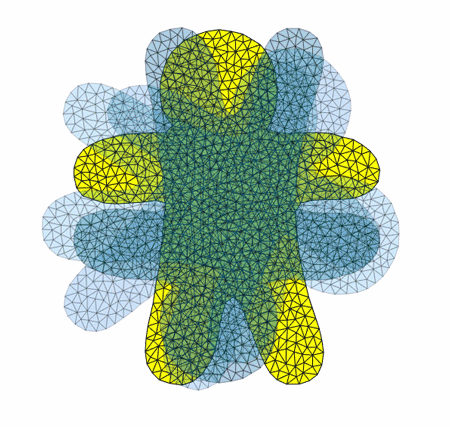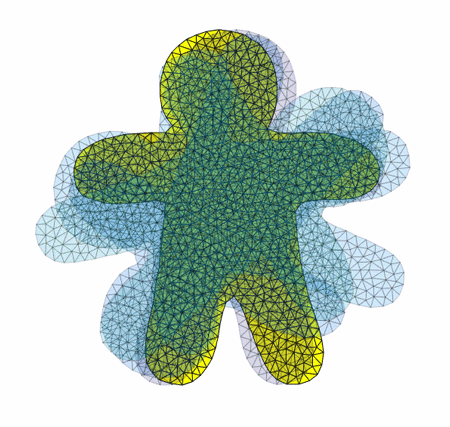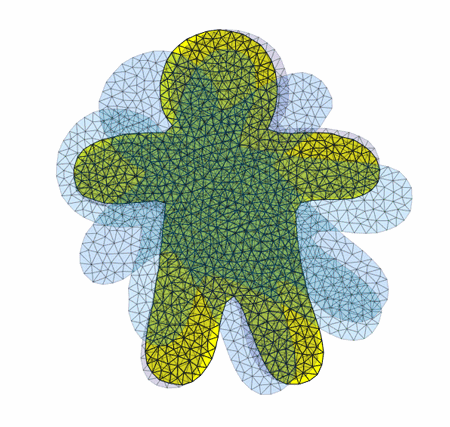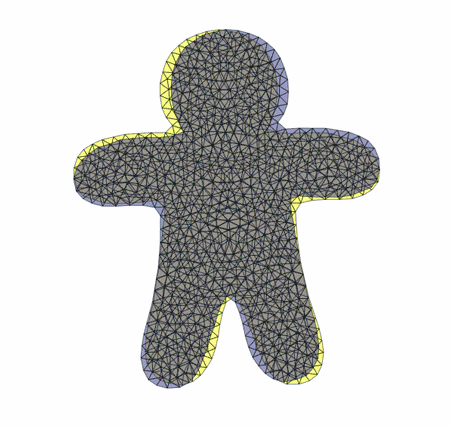
Here're a couple visualizations of the algorithm in progress:

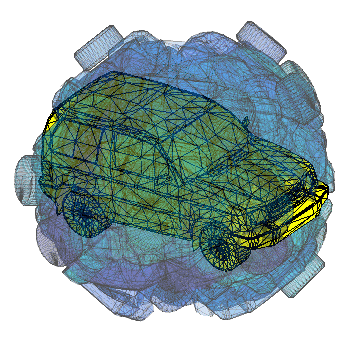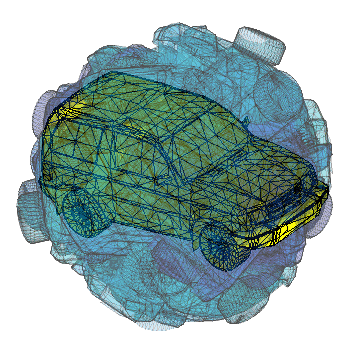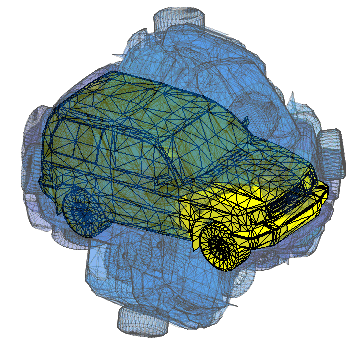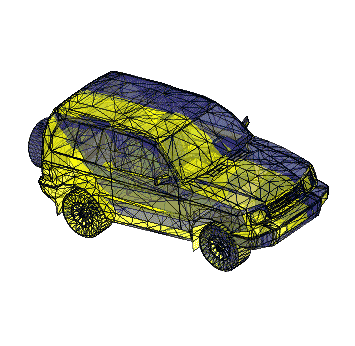

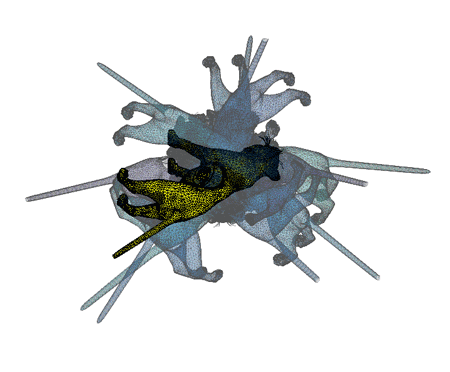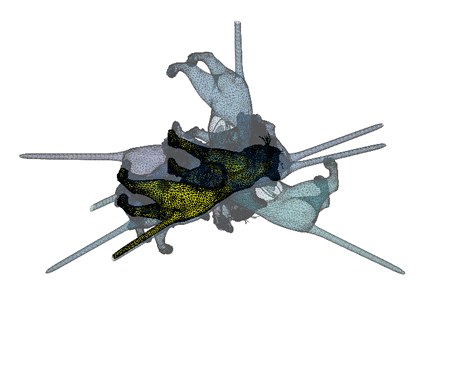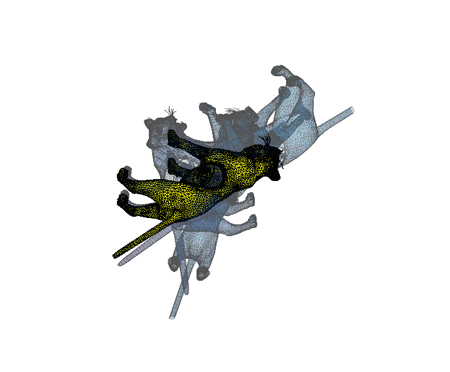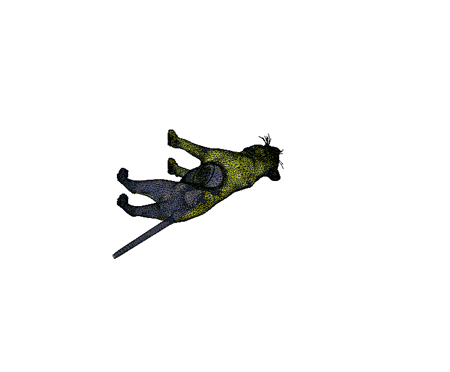
Implementing this with straight matlab, you just need knnsearch and procrustes (or gptoolbox's fit_rigid.m, see use in my icp.m implementation). I guess I'll call it Iterative Closest Upside-down Point (ICUP).