Wave equation on surfaces

Alec Jacobson

July 21, 2015

weblog/

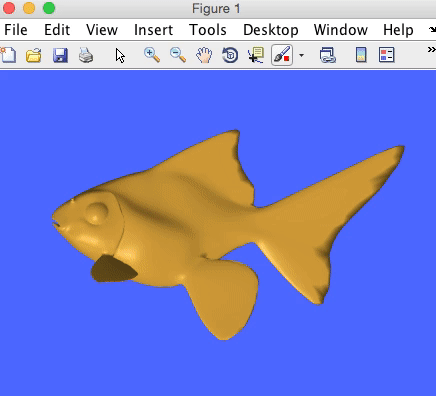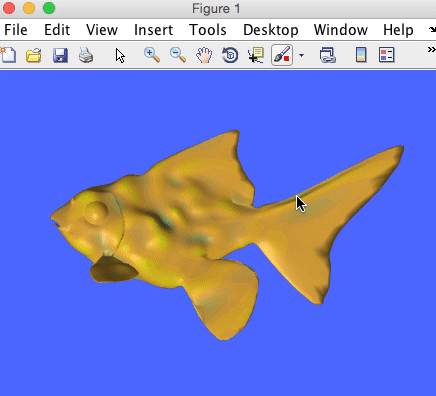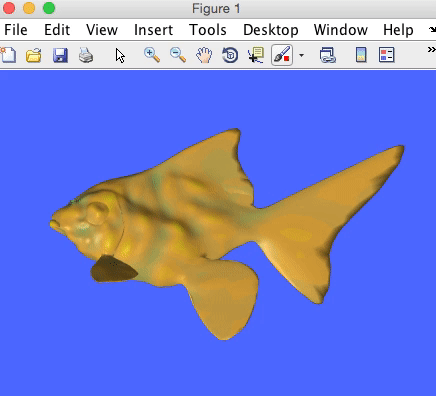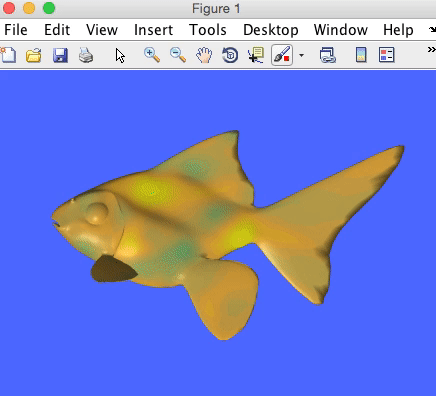
Inspired by a course Misha Kazhdan gave at SGP this year, I started playing around with the wave equation on surfaces. Below is a simple matlab demo:

The core formula here is to update the "height" H_i (extrusion along normal) at vertices for each time step i based on the last two steps:

((1 + b * dt) * M - a * dt^2 *L) H_i = (M * (( 2 - b * dt) * H_{i-1} - H_{i-2}));

b is the dampening factor, dt is the time step size, M is the mass matrix, 1/sqrt(a) is the speed of the wave, L is the cotangent Laplacian, H_i is the unknown heights, H_{i-1} and H_{i-2} are the heights at the previous two time steps. This is discretization with implicit time stepping of the wave equation:

∂²/∂t² u = a∆u - b ∂u/∂t

There's surely a more canonical place to find this, but I liked the description in "Fast and Exact (Poisson) Solvers on Symmetric Geometries" [Kazhdan 2015].

Save in wave_demo.m

function wave_demo(V,F)
  V = bsxfun(@minus,V,mean(V));
  V = V./max(abs(V(:)));
  V(:,end+1:3) = 0;
  N = per_vertex_normals(V,F);
  L = cotmatrix(V,F);
  M = massmatrix(V,F);
  M = M / max(abs(M(:)));

  dt = 0.0075;
  % 1/sqrt(a) is the speed of the wave
  a = 1;
  H = zeros(size(V,1),1);
  % dampening
  b = 0.05;
  A = ((1+b*dt)*M - a*dt^2*L);
  % Pre-factor
  [cL,p,cS] = chol(A,'lower');
  cU = cL';
  cP = cS';
  cQ = cS;
  chol_solve = @(X) cQ * (cU \ (cL \ ( cP * X)));
  G = H;
  G_m1 = G;      

  [VV,FF,S] = loop([V+bsxfun(@times,G,N) H],F);
  tsh = trisurf(FF,VV(:,1),VV(:,2),VV(:,3),  ...
    'FaceColor','interp','FaceLighting','phong', ...
    'EdgeColor','none','CData',VV(:,4));
  tsh.SpecularStrength = 0.2;
  tsh.SpecularExponent = 100;
  tsh.ButtonDownFcn = @ondown;

  CM = parula(30);colormap(CM(end-11:end,:));
  set(gcf,'Color',[0.3 0.4 1.0]);
  set(gca,'Visible','off');
  l = light('Position',[-0.4 -0.4 1.0],'Style','infinite');
  axis equal;
  axis manual;
  expand_axis(1.2);
  view(2);
  caxis([-max(abs(H)) max(abs(H))]);
  T = get(gca,'tightinset');
  set(gca,'position',[T(1) T(2) 1-T(1)-T(3) 1-T(2)-T(4)]);

  t = 0;
  draw_t = 0;
  tic;
  while true
    G_m2 = G_m1;
    G_m1 = G;
    G = chol_solve(M*((2-b*dt)*G_m1 - G_m2 + dt*0));

    t = t+dt;
    draw_t = draw_t+toc;
    if draw_t > 0.033
      VV = S*[V+bsxfun(@times,G,N) G];
      tsh.Vertices = VV(:,1:3);
      tsh.CData = VV(:,4);
      title(sprintf('t: %g, max(H): %g',t,max(abs(G))),'FontSize',15);
      drawnow;
      tic;
      draw_t = 0;
    end
  end

  function ondown(src,ev)
    H = a/10*mean(diag(M))*(M\(S'*sparse( ...
      knnsearch(VV(:,1:3),ev.IntersectionPoint,'k',2),1,[1;-1],size(VV,1),1)));
    G = G+H;
  end
end