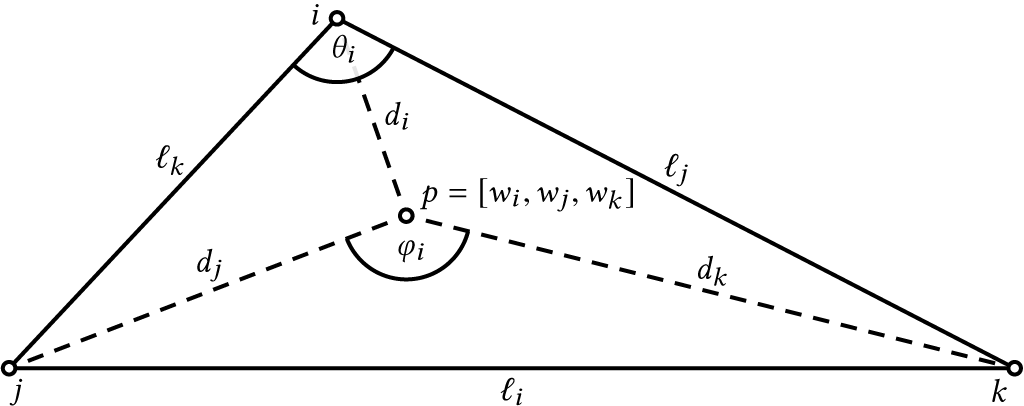
Suppose we are given a triangle \(ijk\) with known metric --- so that \(\ell_i ∈ \mathbb{R}^+\) is the length of the edge opposite corner \(i\) --- and a point \(p\) within this triangle identified by barycentric coordinates \([w_i,w_j,w_k]\). We are interested in deriving expressions for the distance \(d_i\) from \(p\) to the corner \(i\) and the internal angle \(φ_i\) subtended by the side \(jk\) at \(p\).

Momentarily embed the triangle in \(\mathbb{R}^2\); the choice of translation and rotation are irrelevant. We can write the point-to-point squared distance expression in terms of barycentric coordinates: $$ d_i^2 = ‖ \mathbf{p}_i - w_i \mathbf{p}_i - w_j \mathbf{p}_j - w_k \mathbf{p}_k ‖². $$ Because the barycentric coordinates sum to one (\(w_i+w_j+w_k = 1\)), we can simplify this to: $$ \begin{align} d_i^2 &= ‖ \mathbf{p}_i - (1-w_j-w_k) \mathbf{p}_i - w_j \mathbf{p}_j - w_k \mathbf{p}_k ‖², \\ &= ‖ w_j (\mathbf{p}_i-\mathbf{p}_j) + w_k (\mathbf{p}_i-\mathbf{p}_k) ‖². \end{align}$$ Expanding the square produces an expression in terms of scalar lengths and angles: $$ d_i^2 = w_j² \ell_k² + w_k² \ell_j² + 2 w_j w_k \ell_j \ell_k \cos θ_i, $$ where \(θ_i\) is the corner angle at \(i\).
The Law of Cosines states that: $$ 2 \ell_j \ell_k \cos θ_i = -\ell_i² +\ell_j² + \ell_k². $$ Substituting this above, we have an expression for \(d_i²\) that only involves the side lengths and barycentric coordinates:
Consider the sub-triangle \(jpk\), we can express the cosine of the subtended angle \(φ_i\) in terms of the analogously derived lengths \(d_j,d_k\) via the Law of Cosines:
As far as I can tell, there is no way to avoid the square root arising from this expression.