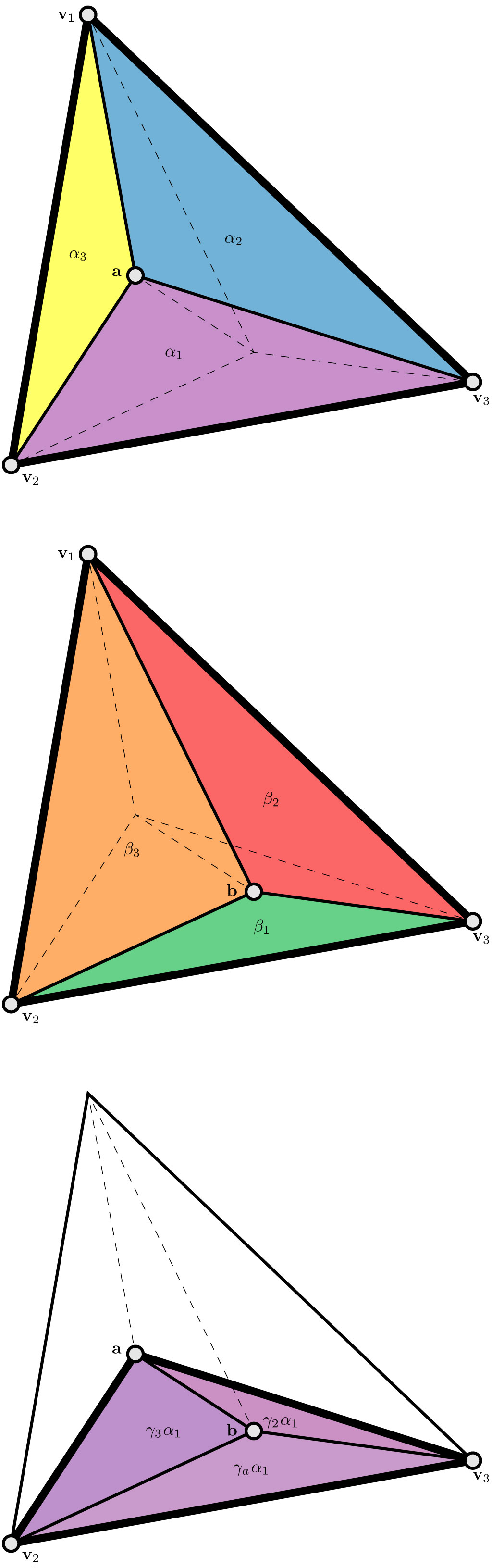
Given a non-degenerate triangle with corner positions at V = (v₁,v₂,v₃) and two interior points a,b with barycentric coordinates α and β. We would like to identify which subtriangle (a,vi,vi+1) within b lies, and what are its "new" barycentric coordinates γ in this subtriangle.

Assume that b lies within subtriangle (a,v₂,v₃), then
V β = [a v₂ v₃] γ
V β = V [α δ₂ δ₃] γ
β = [α δ₂ δ₃] γ
[α δ₂ δ₃]⁻¹ β = γ
This system is easily inverted:
[α₁⁻¹[1 -α₂ -α₃]ᵀ δ₂ δ₃] β = γ
[β₁/α₁ β₂-β₁α₂/α₁ β₃-β₁α₃/α₁] = γ
If γ≥0, then our assumption was right. Otherwise, try again with
[δ₁ a δ₃]⁻¹ β = γ
and perhaps again with
[δ₁ δ₂ a]⁻¹ β = γ.
As a side-note, working with barycentric coordinates I consistently find that it's useful to momentarily assume that you have an embedding for the triangle (in this case the non-singular matrix V).