During the SIGGRAPH review process a submitted paper is supposed to receive 5 reviews. Sometimes a paper accidentally receives ≥5 initial reviews. Usually because of sending out too many parallel invitations to non-committee reviewers. My sense is that this has increased since SIGGRAPH started the two-factor conflict-of-interest identification system. I'd always been suspicious that getting too many reviewers actually hurts a paper's chance of acceptance.
One argument for this is that the review process is more akin to aggregating identified flaws of a paper than whipping up excitement about the contributions. That seems plausible but difficult to prove.
Here I'll try to make a different, more basic statistical argument.
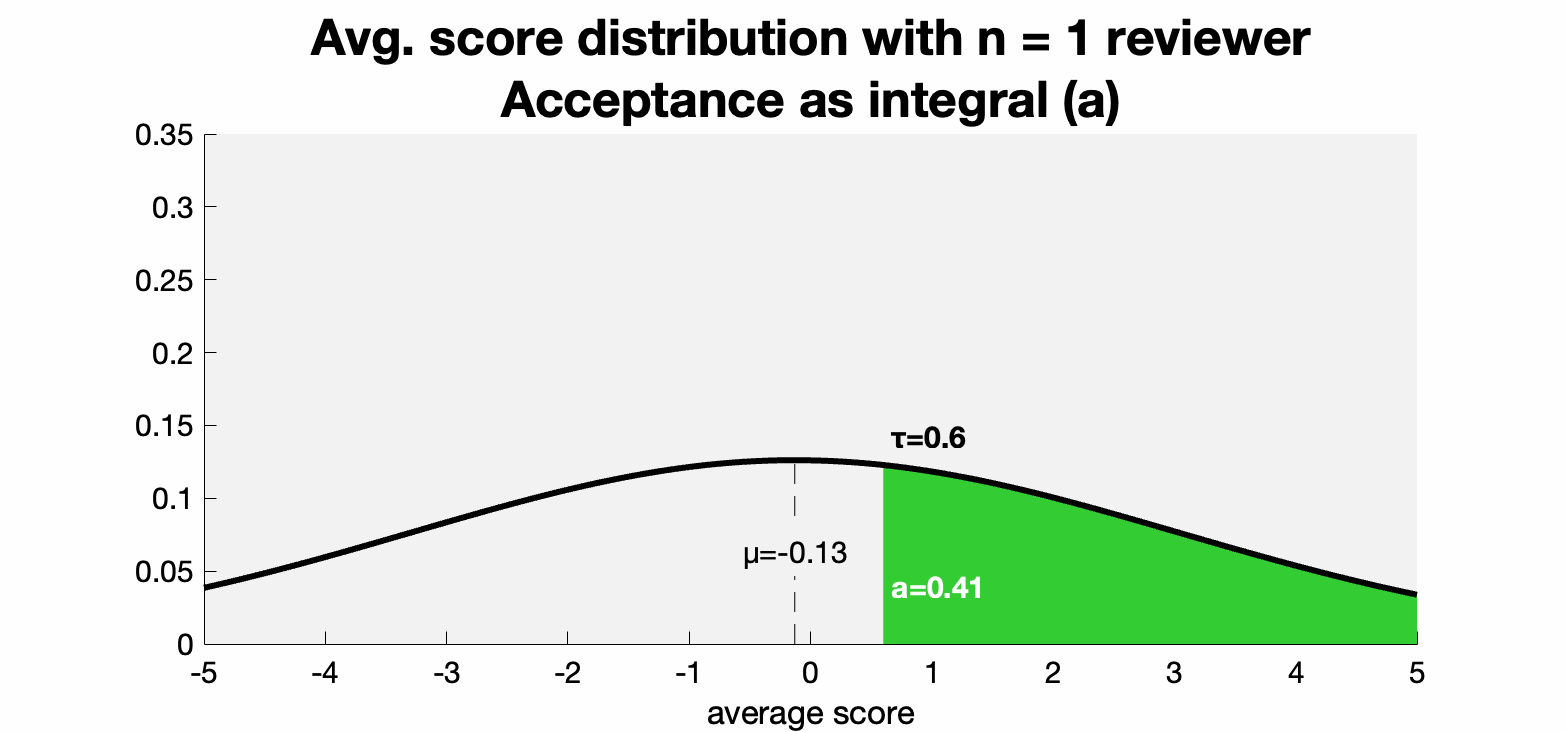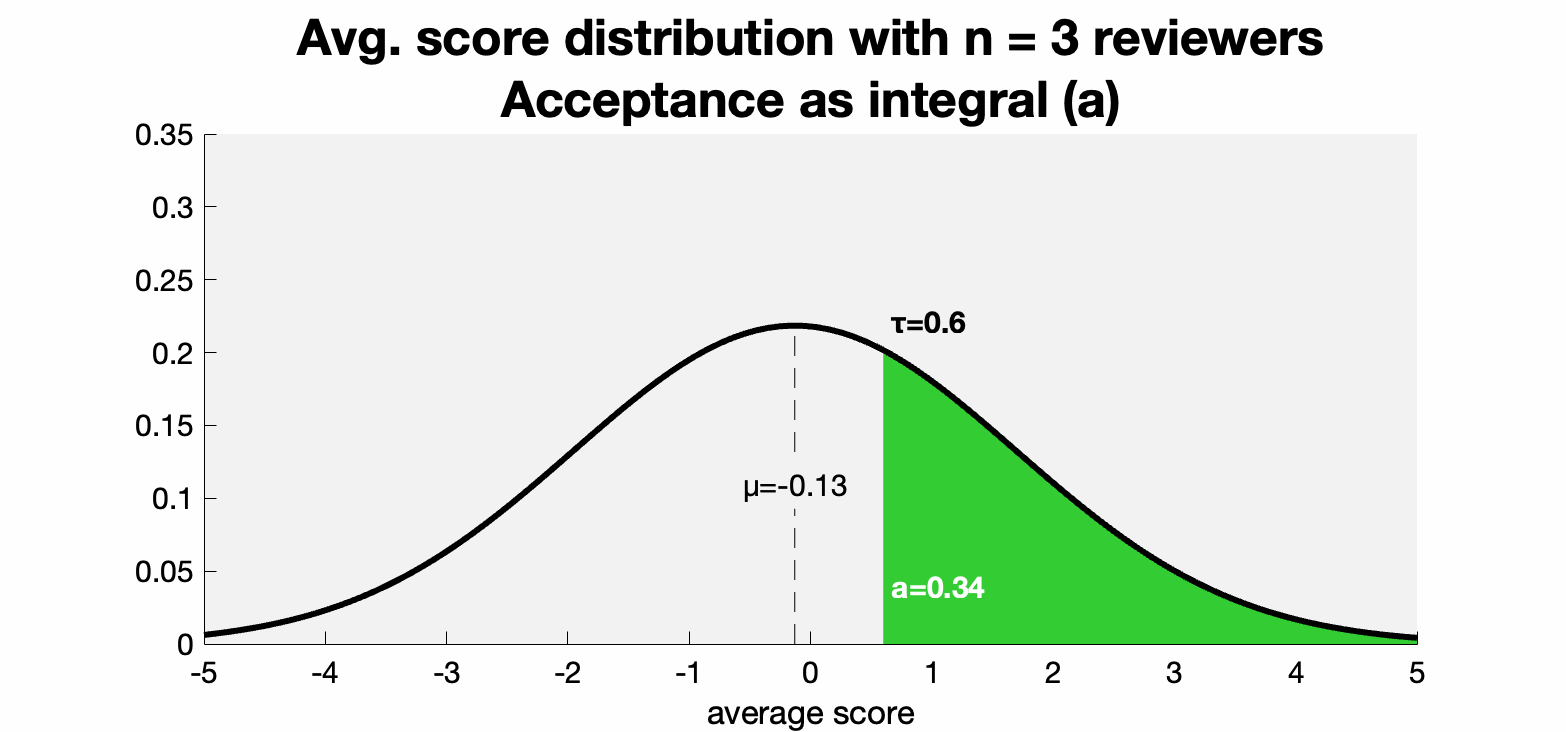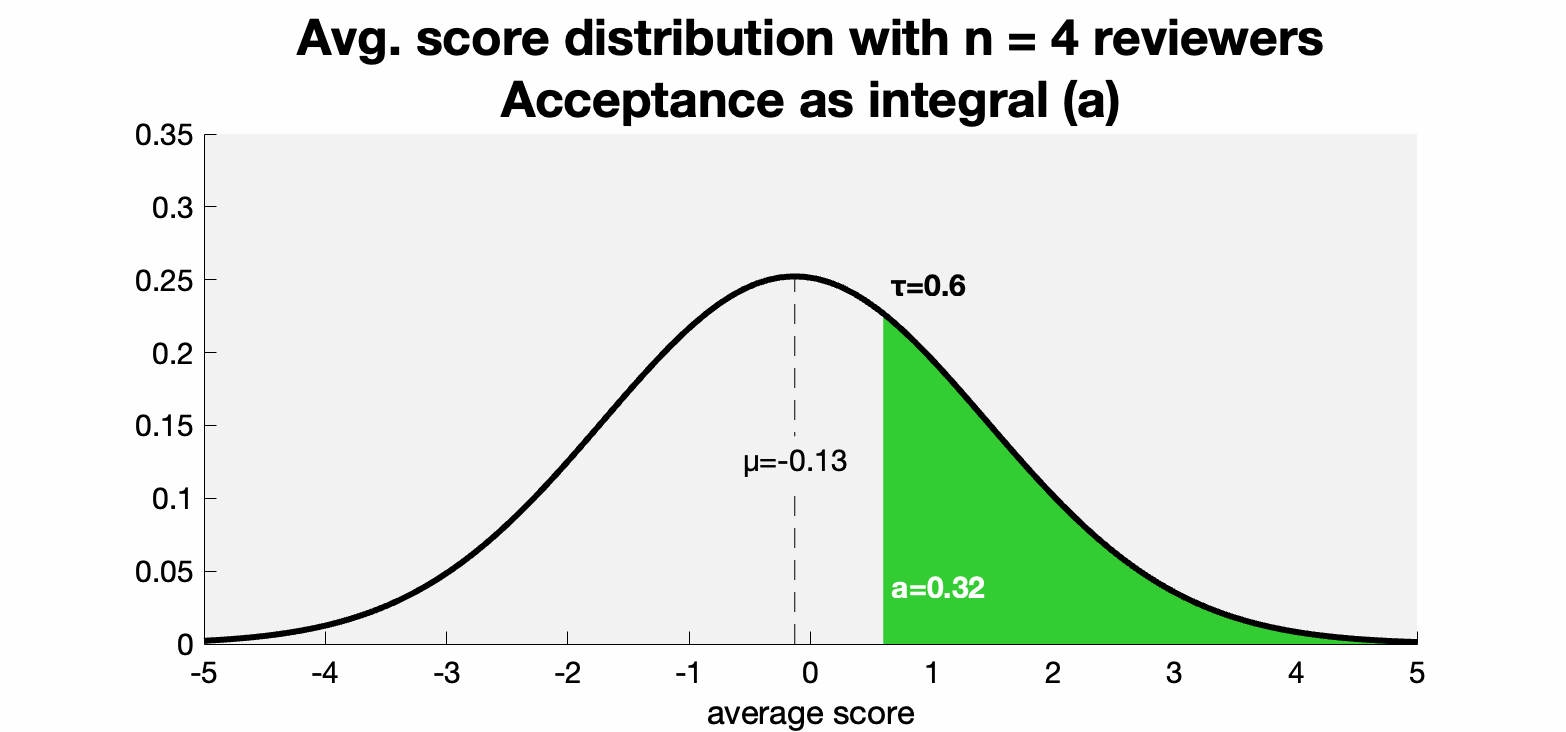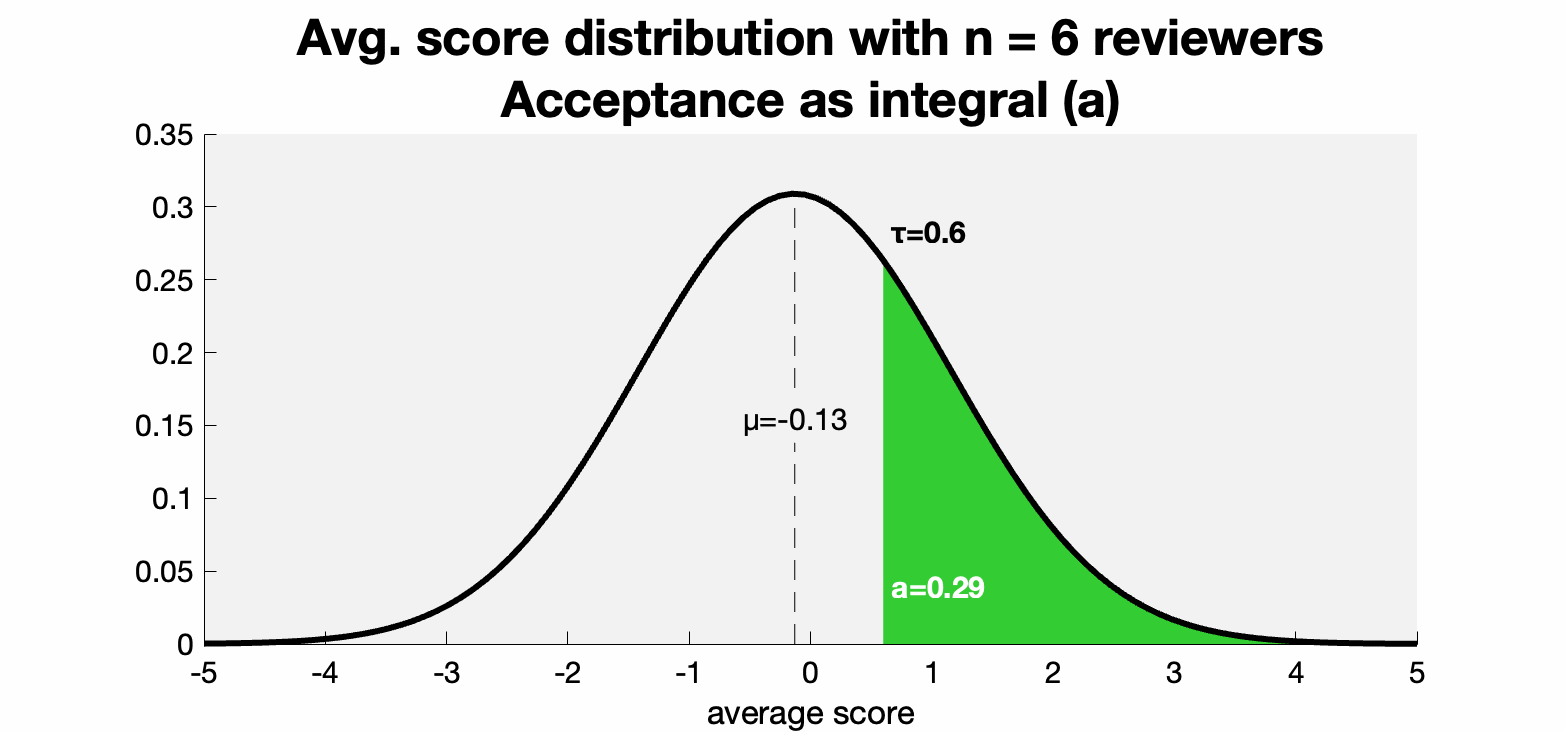
As a simplified model of the review process, let's assume that each reviewer picks a score in ℝ for the paper and the paper gets accepted if the average score is above some threshold τ. For SIGGRAPH, the scores are in [-5,5] and a good estimate for τ=0.6.
Our prior on the reviewer's score of a paper is that it will be drawn from a normal distribution N(μ=μ₁,σ²=σ₁²) with an average score of μ₁ and variance σ₁². The average score of n reviewers drawn from this distribution will be a normal distribution with the same mean but smaller variance N(μ=μ₁,σ²=σ₁²/n).
A paper can either be accepted or rejected, and the probability that it is under these distribution is the area under the probability distribution to the left of τ:
∫_τ^∞ 1/√(2πσ²) exp( -(x-μ)/(2σ²) ) dx
which can be evaluated numerically for various n values.
Based on some historical numbers, we can set good estimates for the threshold τ=.6 and μ=-.13. Historically, the majority of SIGGRAPH papers get 5 reviews and the acceptance rate is around 30%. So this implies σ₁²/5 ≈ 2. Plugging in these estimates we can plot the change in acceptance rate as the variance tightens with each review:

The basic fact that we're visualizing here is that if the expected review score is below the threshold then adding reviewers decreases the variance around it and subsequently decreases the chance of acceptance.
In particular, for n=5 and n=6 we see a drop from 30.29% to 28.59%. Not huge, but not nothing. Given the opportunity, I'm confident every author would prefer a 1.7% advantage.
If you're confident that your super special submission is a "good paper" not drawn from the general pool of papers but rather from a pool of papers with μ>τ then you should prefer additional reviews.
As policy, we don't know which papers are "good" a priori so using the general pool is the only reasonable prior. As such, giving certain papers extra reviews is unfair. Even if assigning extra reviewers is done uniform randomly --- so that we might say it is "fair" in the sense that after many submissions every author experiences the same average disadvantages --- it is still unfair in the more common sense of preventably treating authors differently for this event.