Areas of quadrilaterals within a triangle determined by its circumcenter (or perpendicular bisectors), using matlab
Alec Jacobson
February 11, 2010
First, I need to locate the circumcenter of the triangle. The circumcenter is the center of the circle circumscribing the three points of the triangle. Thus, it is equidistance from all three points.
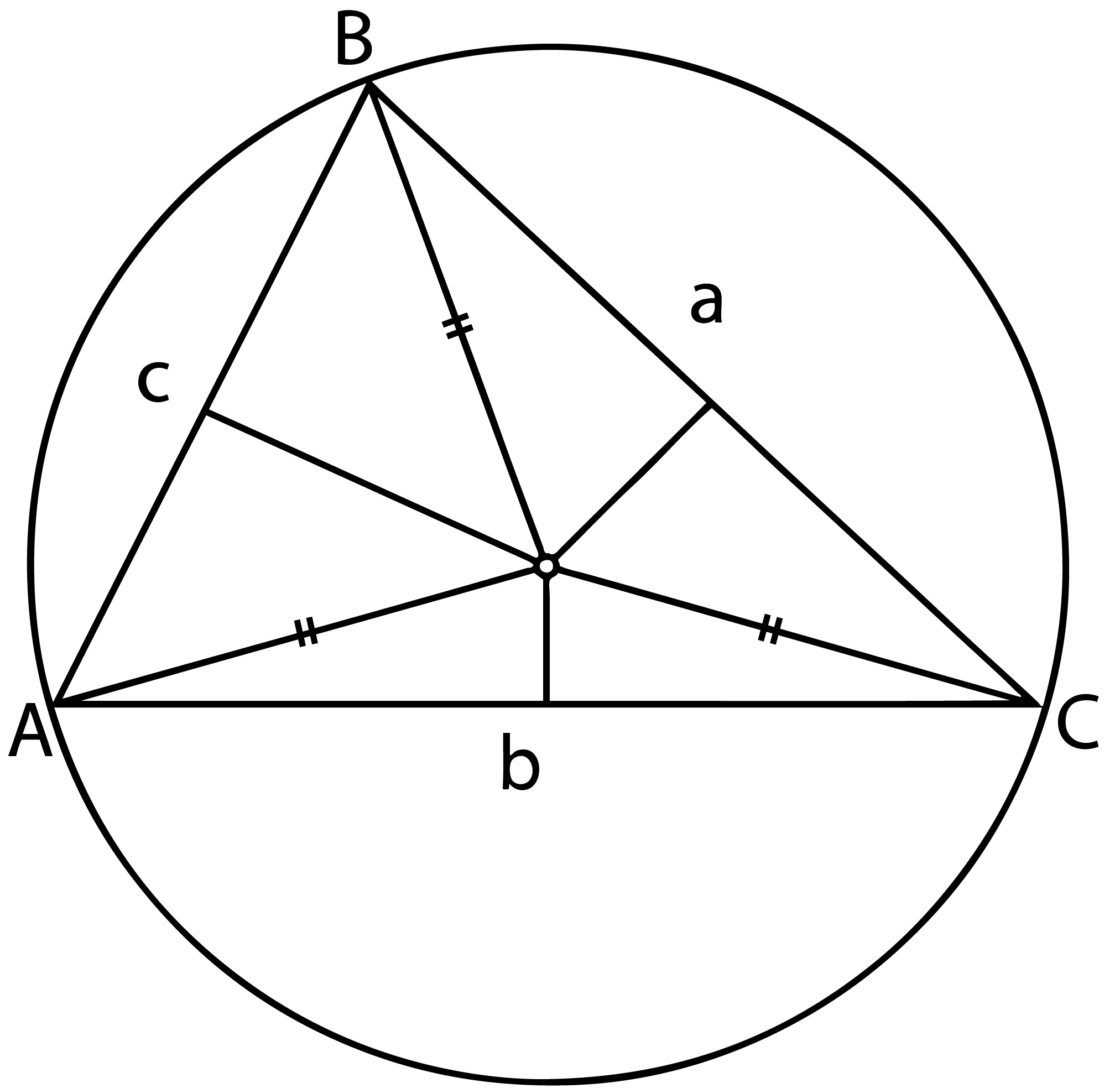I do not need the actual world coordinates of the circumcenter, rather it is okay for me to just know the relative distance to each corner. The law of cosines tells me that the relative distance of the circumcenter from the line opposite point A (called a in the picture) is cos A (that is cosine of the angle at A). Likewise for B and C. Knowing these I can convert to barycentric coordinates by multiplying by the opposite edge lengths.
cosines = [ ...
(edge_norms(:,3).^2+edge_norms(:,2).^2-edge_norms(:,1).^2)./(2*edge_norms(:,2).*edge_norms(:,3)), ...
(edge_norms(:,1).^2+edge_norms(:,3).^2-edge_norms(:,2).^2)./(2*edge_norms(:,1).*edge_norms(:,3)), ...
(edge_norms(:,1).^2+edge_norms(:,2).^2-edge_norms(:,3).^2)./(2*edge_norms(:,1).*edge_norms(:,2))];
barycentric = cosines.*edge_norms;
normalized_barycentric = barycentric./[sum(barycentric')' sum(barycentric')' sum(barycentric')'];
A quality of the barycentric trilinear coordinates of a point in a triangle is that they specify the relative area of inner triangles form by connecting the corners to that point. In our case, the triangles made by connecting the circumcenter to each corner. Here, the aquamarine, red, and purple triangles corresponding to points A, B, and C.
Now I find the area of the triangle and then multiple against the normalized barycentric coordinates of the circumcenter to get the areas of each of these inner triangles:
areas = 0.25*sqrt( ...
(edge_norms(:,1) + edge_norms(:,2) - edge_norms(:,3)).* ...
(edge_norms(:,1) - edge_norms(:,2) + edge_norms(:,3)).* ...
(-edge_norms(:,1) + edge_norms(:,2) + edge_norms(:,3)).* ...
(edge_norms(:,1) + edge_norms(:,2) + edge_norms(:,3)));
partial_triangle_areas = normalized_barycentric.*[areas areas areas];
Finally the quadrilateral at each point is built from half of the neighboring inner triangles: the green, blue and yellow quads corresponding to A, B, and C.
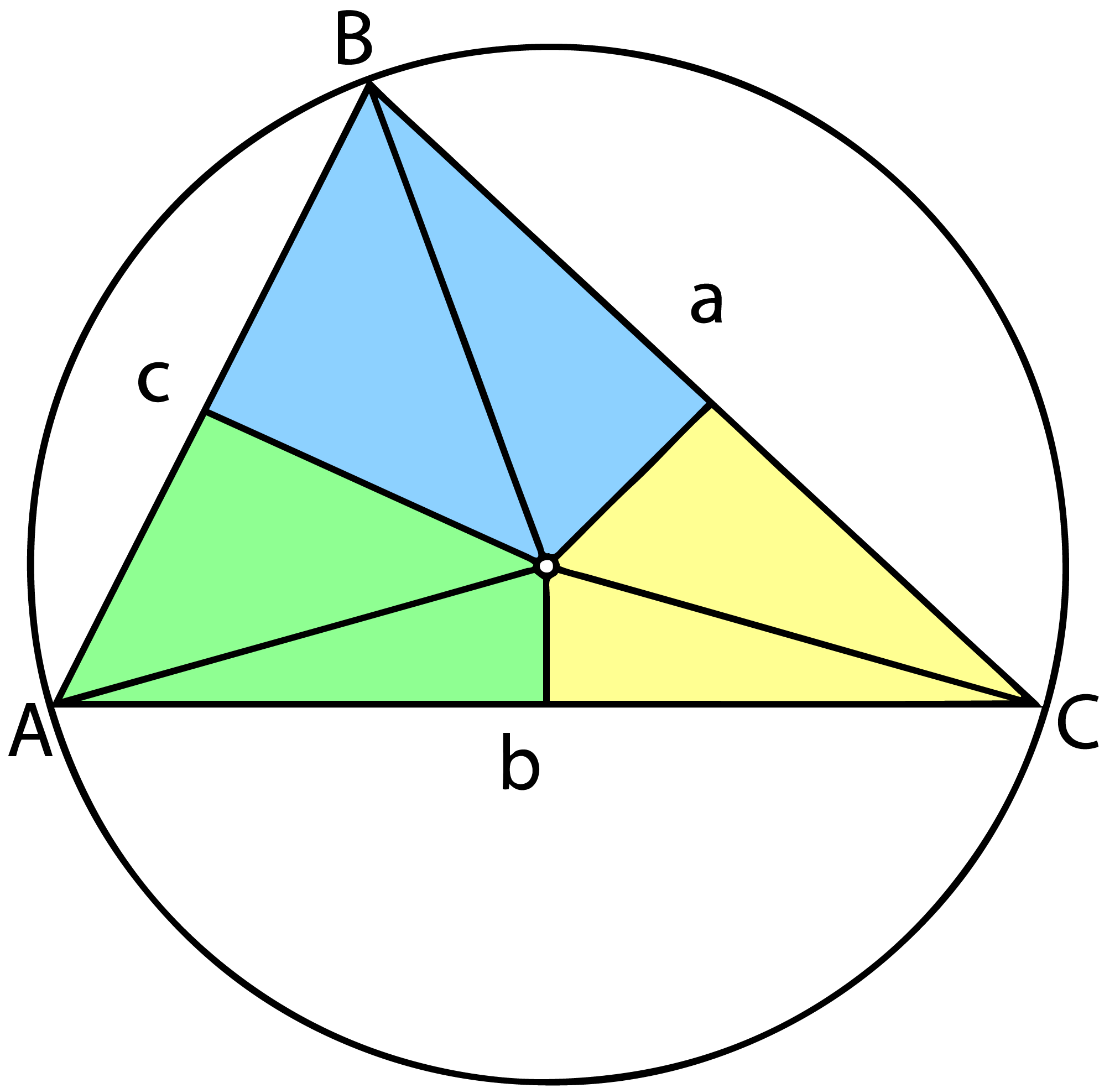Note, that the fact that these inner triangles are cut perfectly in half follows immediately from the fact the the circumcenter is equidistance from each corner. So the last step is just to add up the halves:
quads = [ (partial_triangle_areas(:,2)+ partial_triangle_areas(:,3))*0.5 ...
(partial_triangle_areas(:,1)+ partial_triangle_areas(:,3))*0.5 ...
(partial_triangle_areas(:,1)+ partial_triangle_areas(:,2))*0.5];
Note: I've suffered trying to use mathematic or maple to reduce these steps to a simple algebra formula (I must be mistyping something). As far as I can tell the above steps check out (of course, it only makes sense for cases where the circumcenter is within or on the triangle: i.e. the triangle is not obtuse). I have checked out my equations on maple with the following functions:
mycos:=(a,b,c)->(b^2+c^2-a^2)/(2*b*c);
barycentric:=(a,b,c)->a*mycos(a,b,c);
normalized_barycentric:=(a,b,c)->barycentric(a,b,c)/(barycentric(a,b,c)+barycentric(b,c,a)+barycentric(c,a,b));
area:=(a,b,c)->sqrt((a+b-c)*(a-b+c)*(-a+b+c)*(a+b+c))/4;
inner_triangle:=(a,b,c)->normalized_barycentric(a,b,c)*area(a,b,c);
quad:=(a,b,c)->(inner_triangle(b,c,a)+inner_triangle(c,b,a))/2;
Which then you can run:
simplify(quad(a,b,c));
To see a beautiful long algebra formula for the quadrilateral at point A.
Which in matlab corresponds to:
quads = ...
[-sqrt(-(edge_norms(:,1) + edge_norms(:,2) + edge_norms(:,3)).* ...
(edge_norms(:,1) - edge_norms(:,2) - edge_norms(:,3)).* ...
(edge_norms(:,1) - edge_norms(:,2) + edge_norms(:,3)).* ...
(edge_norms(:,1) + edge_norms(:,2) - edge_norms(:,3))).* ...
(2.*edge_norms(:,2).^2.*edge_norms(:,3).^2 + edge_norms(:,1).^2.* ...
edge_norms(:,2).^2 - edge_norms(:,2).^4 + edge_norms(:,1).^2.* ...
edge_norms(:,3).^2 - edge_norms(:,3).^4)./ ...
(8.*(edge_norms(:,1) + edge_norms(:,2) + edge_norms(:,3)).* ...
(edge_norms(:,1) - edge_norms(:,2) - edge_norms(:,3)).* ...
(edge_norms(:,1) - edge_norms(:,2) + edge_norms(:,3)).* ...
(edge_norms(:,1) + edge_norms(:,2) - edge_norms(:,3))), ...
-sqrt(-(edge_norms(:,2) + edge_norms(:,3) + edge_norms(:,1)).* ...
(edge_norms(:,2) - edge_norms(:,3) - edge_norms(:,1)).* ...
(edge_norms(:,2) - edge_norms(:,3) + edge_norms(:,1)).* ...
(edge_norms(:,2) + edge_norms(:,3) - edge_norms(:,1))).* ...
(2.*edge_norms(:,3).^2.*edge_norms(:,1).^2 + edge_norms(:,2).^2.* ...
edge_norms(:,3).^2 - edge_norms(:,3).^4 + edge_norms(:,2).^2.* ...
edge_norms(:,1).^2 - edge_norms(:,1).^4)./ ...
(8.*(edge_norms(:,2) + edge_norms(:,3) + edge_norms(:,1)).* ...
(edge_norms(:,2) - edge_norms(:,3) - edge_norms(:,1)).* ...
(edge_norms(:,2) - edge_norms(:,3) + edge_norms(:,1)).* ...
(edge_norms(:,2) + edge_norms(:,3) - edge_norms(:,1))), ...
-sqrt(-(edge_norms(:,3) + edge_norms(:,1) + edge_norms(:,2)).* ...
(edge_norms(:,3) - edge_norms(:,1) - edge_norms(:,2)).* ...
(edge_norms(:,3) - edge_norms(:,1) + edge_norms(:,2)).* ...
(edge_norms(:,3) + edge_norms(:,1) - edge_norms(:,2))).* ...
(2.*edge_norms(:,1).^2.*edge_norms(:,2).^2 + edge_norms(:,3).^2.* ...
edge_norms(:,1).^2 - edge_norms(:,1).^4 + edge_norms(:,3).^2.* ...
edge_norms(:,2).^2 - edge_norms(:,2).^4)./ ...
(8.*(edge_norms(:,3) + edge_norms(:,1) + edge_norms(:,2)).* ...
(edge_norms(:,3) - edge_norms(:,1) - edge_norms(:,2)).* ...
(edge_norms(:,3) - edge_norms(:,1) + edge_norms(:,2)).* ...
(edge_norms(:,3) + edge_norms(:,1) - edge_norms(:,2)))];
Note: It seems also that the wikipedia page for the circumscribed circle has a direct formula for the barycentric coordinates of the circumcenter. Though, wolfram's mathworld has an ostensibly different formula. Upon a quick review Wolfram's is at least easily verifiable to be the same as mine (recall these only need to be relative to each other).