Areas of quadrilaterals within a triangle determined by its circumcenter (or perpendicular bisectors), using matlab, part 2
Alec Jacobson
February 13, 2010
Yesterday, I posted some matlab code to determine the areas of quadrilaterals within a triangle determined by its circumcenter. Now, I'm updating to talk about handling obtuse triangles, where the circumcenter is outside of the triangle, i.e. the areas of the quads may be negative. So the formulas from yesterday will work for right angle triangles and acute triangles but might fail for obtuse triangles. We then need a set of areas for obtuse triangles. The areas for a right triangle and a barely right triangle should be at the limit the same, i.e. no jump. To handle this, I noticed that for a right angle triangle the circumcenter is the same as the midpoint along the edge opposite the right angle.
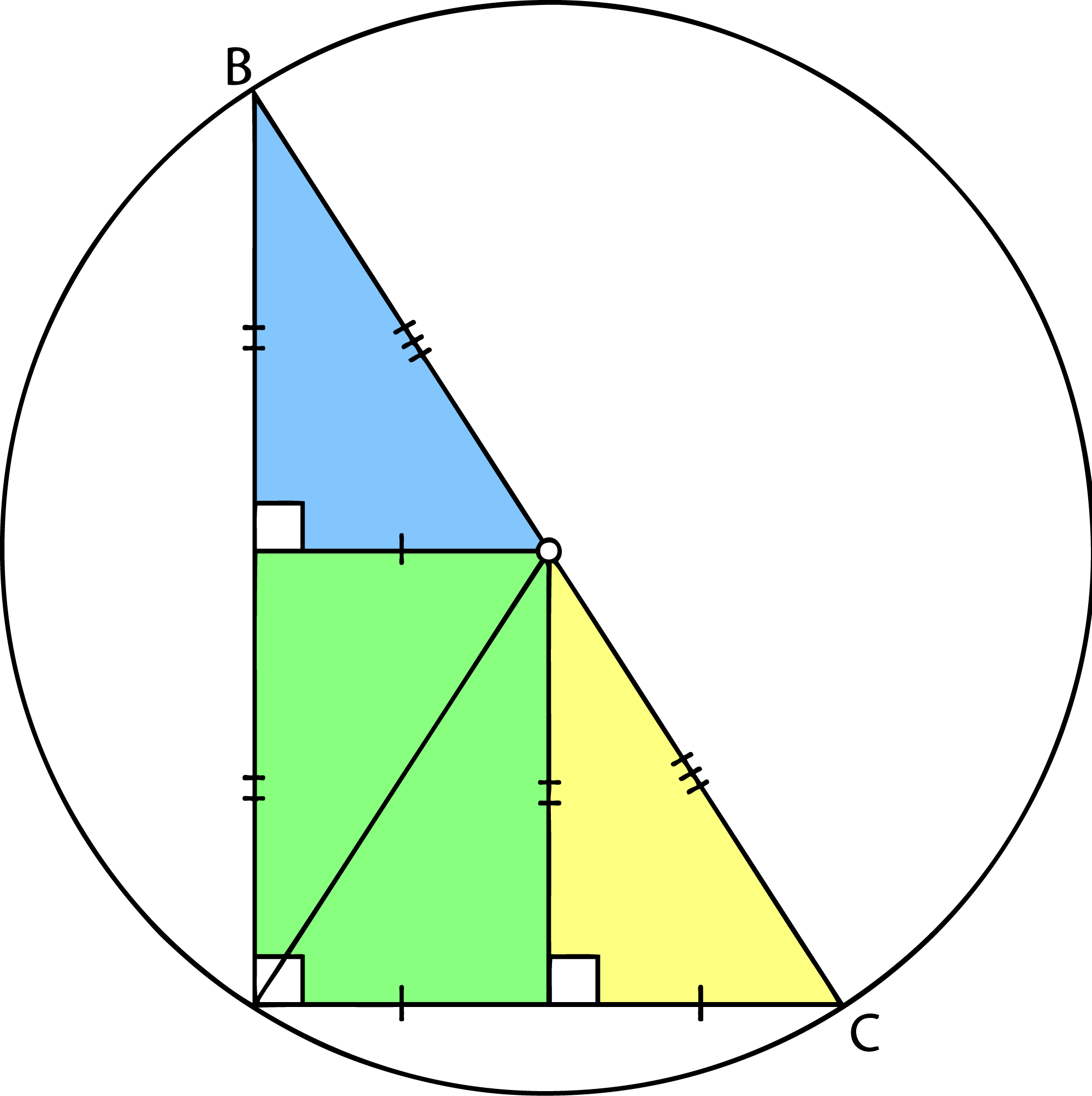Connect the midpoints making three "quads", on at each point (two are collapsed into triangles). Notice that all the inner triangles are congruent and have the same are thus the areas of the green, blue and yellow "quads" are area/2, area/4, area/4 corresponding to point A,B, and C, where area of course is the area of the entire triangle.
Now, do the same midpoint connections for an obtuse triangle:
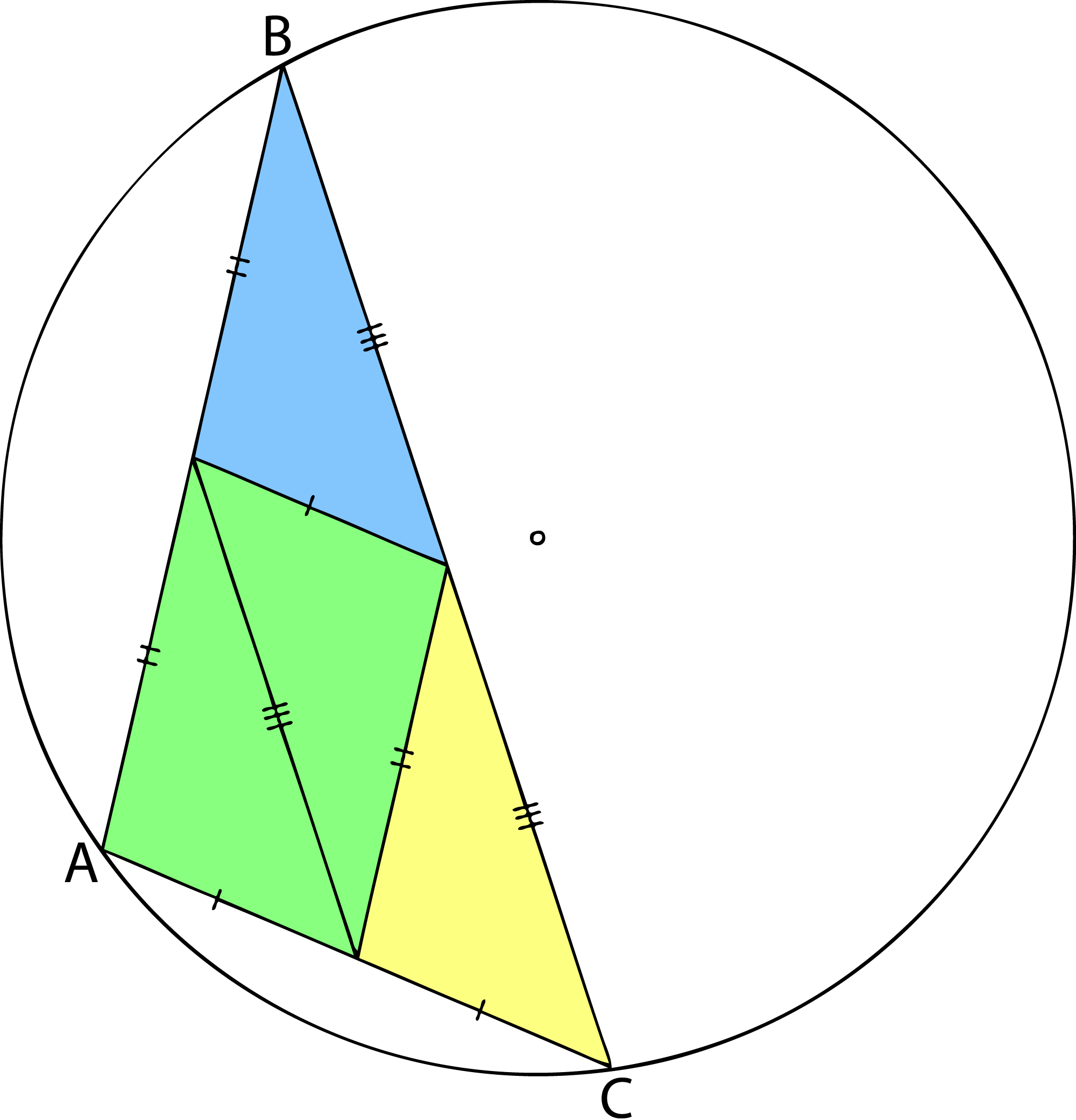The circumcenter is no longer lined up with the midpoint along the longest side, but you do have the same congruent inner triangles and corresponding "quads". Again the areas of the green, blue and yellow "quads" are area/2, area/4, area/4 corresponding to point A,B, and C, where area of course is the area of the entire triangle.
If you have already done the first step in my last post, to handle the right and acute triangles, then to zap out the obtuse triangles with the "corrected" quad areas use:
quads(cosines(:,1)<0,:) = [areas(cosines(:,1)<0,:)*0.5, ...
areas(cosines(:,1)<0,:)*0.25, areas(cosines(:,1)<0,:)*0.25];
quads(cosines(:,2)<0,:) = [areas(cosines(:,2)<0,:)*0.25, ...
areas(cosines(:,2)<0,:)*0.5, areas(cosines(:,2)<0,:)*0.25];
quads(cosines(:,3)<0,:) = [areas(cosines(:,3)<0,:)*0.25, ...
areas(cosines(:,3)<0,:)*0.25, areas(cosines(:,3)<0,:)*0.5];