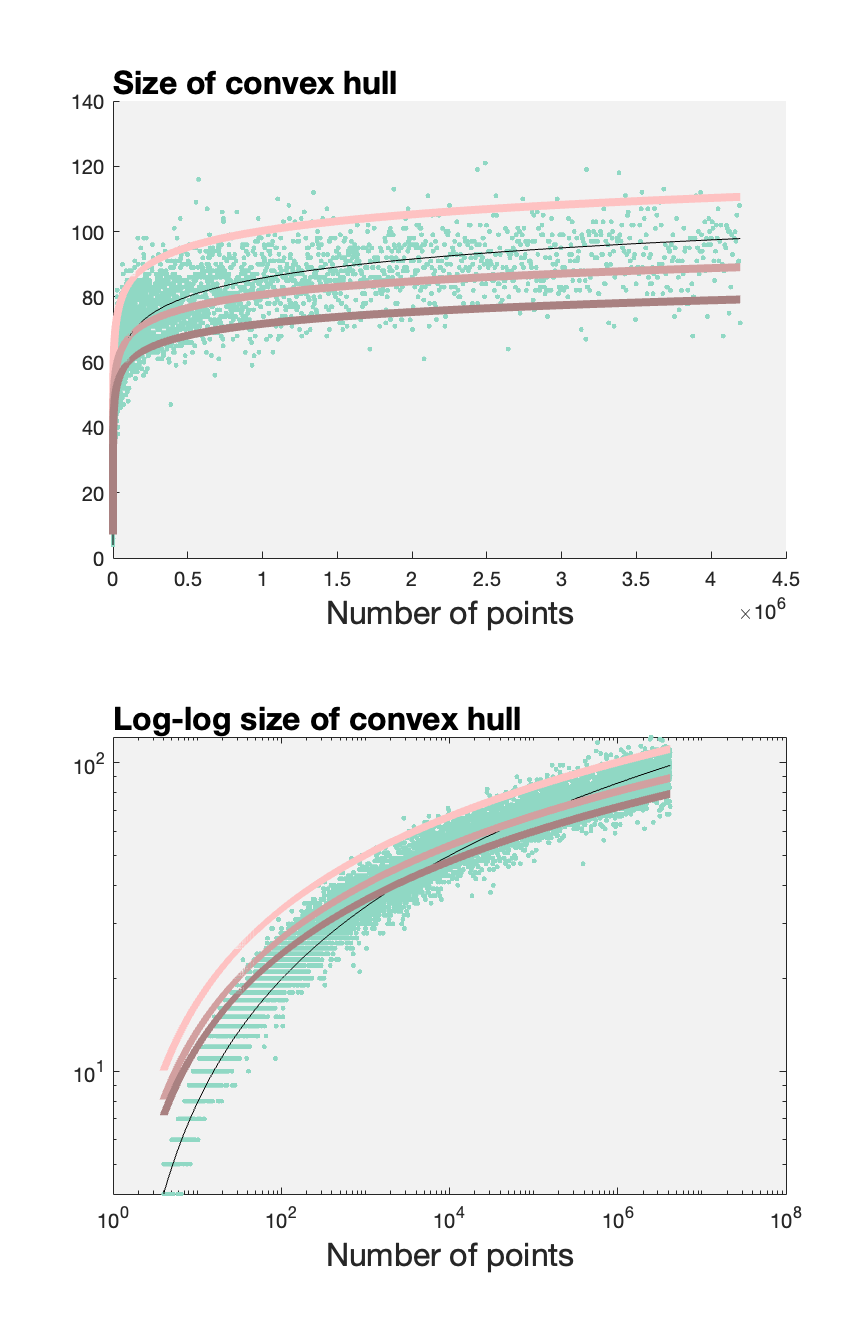
Suppose you have $m$ points in $\mathbb{R}^3$ that are drawn from a normal distribution. Construct their convex hull. Many of the points will be on the interior, so the size of the convex hull $n$ will generally be much smaller than the set of points.
This morning I couldn't find the theoretical result which I'd sworn I could find in the past, so I resorted to doing some randomized experiments.

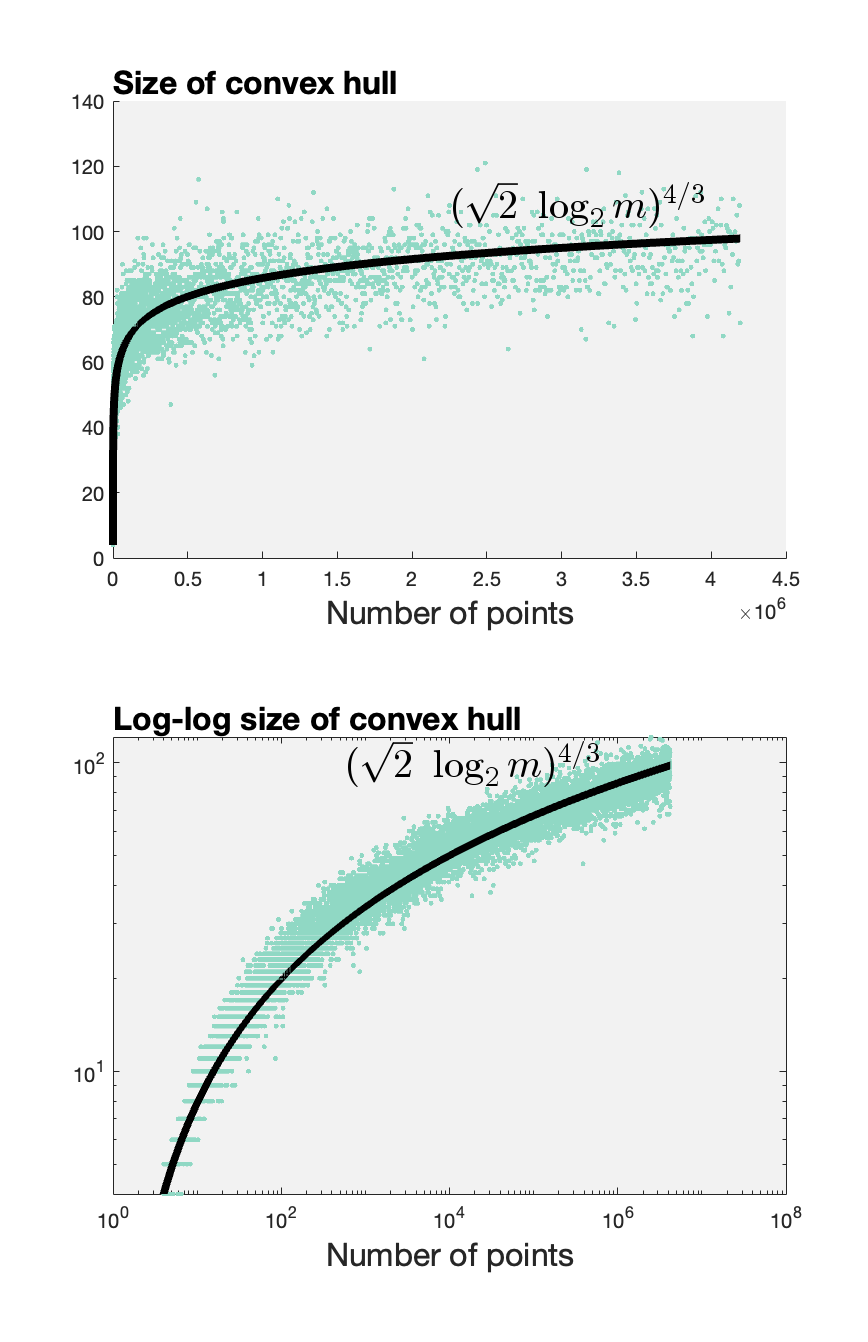
The top plot shows that the size of the convex hull is clearly sublinear. The log-log plot on the bottom shows that it's not polynomially sublinear. This hinted to me that the relationship would look something like: $$ n \sim (b \log_2 m)^a $$ for some constants $a$ and $b$.
When $m=4$ we must have that $n=4$, so we can solve for $b$ as a function of $a$: $$ b = 4^{1/a}/2 $$.
Then I ran a regression on $a$ using the teal dots above and found that $a \approx 1.333$. Rounding to a tidy fraction $a=4/3$ we get $b=\sqrt{2}$. The black fit line above corresponds to my candidate model: $$ n \approx (\sqrt{2} \log_2 m)^{4/3}. $$
After doing all this I did manage to find some theoretical results. For example, "The convex hull of a uniform sample from the interior of a simple d-polytope" by Barthold F. Van Wel cites "Sur l'enveloppe convexe des nuages de points aleatoires dans $\mathbb{R}^{n}$" by H. Raynaud 1970 for normal distribution case. While it's clear from the Van Wel reference what Raynaud says about the number of faces on the convex hull. I can't understand the french paper well enough to tell if Raynaud explicitly gives a formula for vertices. For now I'm a bit skeptical of a good match because the number of faces is $f = O(\log m)$ and via Gauss-Bonnet the number of vertices should $n = O(f)$, implying $n = O(\log m)$ which doesn't include the exponent I'm seeing experimentally. And no simple choice of $b$ gets $b \log m$ to fit my data well.
After sharing with some better French readers, it seems the corollary in the Raynaud paper would be: $$ n \sim \frac{2^d (\pi \log{m})^{(d-1)/2} d^{-1/2}}{n-1} \approx (5.0289 \log_2{m})^1. $$ And, well, this is a pretty bad fit to the experimental data.