
The Symposium on Geometry Processing is a yearly conference where computer scientists present advances in algorithms for analyzing, modelling, simulating and otherwise processing shapes on the computer. Shapes could be geometry in any potential sense, but this conference primarily focuses on the surfaces of 3D solid objects. And the primary representation for these surfaces on the computer is the triangle mesh: a collection of 3D points on the surface called vertices connected in triplets to form triangular patches of the surface.

The Symposium on Geometry Processing is my academic home, so it was a special honor to give a keynote there. I found an old photograph — not necessarily the most embarrassing one — of me giving my very first academic talk at SGP in 2010. I was incredibly nervous (and I remember exactly who was really mean to me in the Q&A session 👀).
The Symposium on Geometry Processing is the place where we can geek out about triangle meshes. It's where we can go into really intricate detail about the meshes that we study. The same day I gave a keynote at SGP this year, I also gave a paper talk presenting something new about meshes.
I work with triangles a lot. I've been developing libigl for close to 15 years. Libigl is a C++ library for processing primarily triangle meshes.

I could spend hours working with triangle meshes. A few years back, I was at a coffee shop, toiling away at programming some triangle mesh processing algorithm on my laptop. When I'm really stuck debugging I tend to sigh a lot, and I must have been loud enough to bother the people next to me. When finally everything was working and I saw what I needed to see on the screen, I was so relieved and let out a big, "Yes!". The guy in the coffee shop next to me leaned over at my screen and said, "All of that for an elephant."
Today is a really wonderful time to be doing geometry processing research. The stakes are higher than ever. Digital geometric data has entered our lives in so many ways.
Over half of American children are playing games on Roblox. Whether we would like it or not, children are making and selling games on Roblox raising new economic and child-labour right questions. The Roblox platform is also realizing some form of the "metaverse." Walmart is making moves to sell physical goods inside of Roblox, and IKEA is attempting to gamify the experience of working at IKEA.
Meanwhile, 3D printing has come so far from a decade ago when the computer graphics research community surged with excitement. You can buy a 3D printer today for $62.77. Companies like nTopology are securing massive investments to change the way we approach advanced manufacturing. The possibility for 3D printed weapons which evade security measures has also changed our society and laws.
Digital geometry has changed the way that we communicate with each other. For example, there are virtual reality applications for demonstrating the effects of COVID-19. The New York Times frequently uses 3D reconstructions and visualizations in their interactive scroller articles to explain the latest world disaster (e.g., "The Surfside Condo Was Flawed and Failing. Here’s a Look Inside."). Independent investigators — like those at Forensic Architecture — use geometric reconstructions to question the authenticity of state or police accounts of events (e.g., "Destruction of Medical Infrastructure in Gaza").
When we look at the splashiest recent advances in 3D geometry, we're not seeing a lot of triangle meshes. For example, Neural radiance fields (NeRFs) were a dramatic leap forward in 3D reconstruction from images. InstantNGP made fitting NeRFs fast enough for convenient use. And more recently, Gaussian Splatting exchanged the neural representation for Gaussians to dramatically decrease rendering time.
The New York Times immediately experimented with using InstantNGP to improve 3D portraiture. Last year McDonald's released a commercial directed by Karen X Cheng that used NeRFs in a creative way.
Gaussian splats viewers have been reimplemented many times over, and web browser-based version are particularly compelling. New representations like NeRFs and Gaussian Splatting are making a big impact.
As triangle mesh researchers, we may feel lost and kind of obsolete. What is our role now? Should we give up on triangle meshes and just rebuild our geometry processing pipelines on whatever new representation is trending? "Geometry Processing with Deep Signed Distance Fields." "Geometry Processing with Neural Radiance Fields." "Geometry Processing with Gaussian Splatting."
Another alternative would be to double down hard on identifying the one true representation. We see this attitude manifest in papers as feature tables comparing different representations and concluding that a chosen representation is ideal because it's the only one that can do all of the tasks in the table. In reality, these criteria are often cherry-picked and incomplete.
My stance is that we should choose not to see new representations as a problem. We should embrace the diversity of different function spaces for representing geometry or the quantities defined over some geometry.
Leaving the representation decision free will also give us the freedom to care more about what comes before and after our pipelines. In particular, I'm excited to see our community shift more focus toward tracking error and uncertainty through our geometry processing pipelines. I'll now provide some evidence that we're already moving in this direction and that we're good at using diverse function spaces to our advantage.
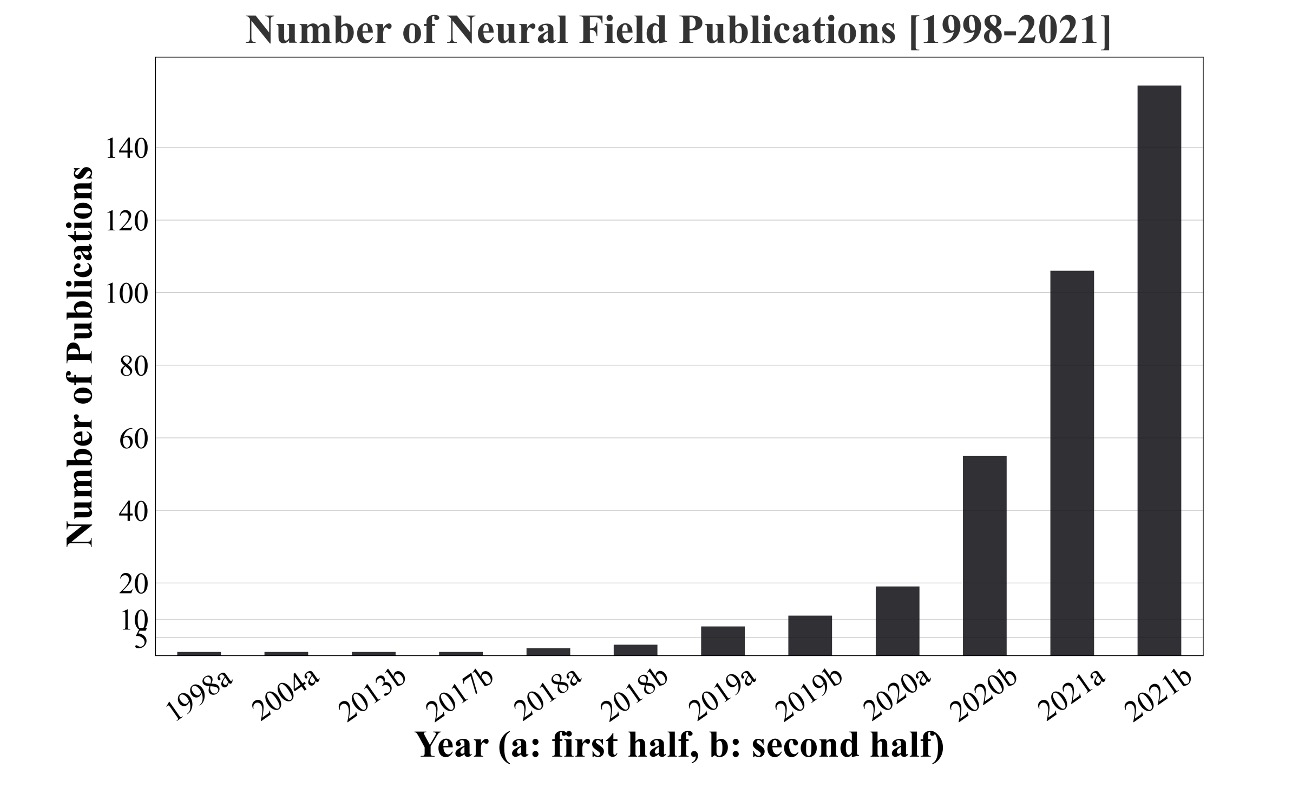
Neural fields have completely exploded in the last few years. The number of publications is skyrocketing. Given the success of neural fields, and the relative decline of interest in triangle meshes, I've been bugging the geometry research students at the University of Toronto with the following line of questions: "We're doing research on triangle meshes right now. Are we still going to be using triangle meshes in five years? Okay, sure, we all agree, of course we will in five years. How about in 50 years? How about in 100 years?"
But what really is the alternative to triangle meshes? What are we talking about when we say using something other than a triangle mesh to represent a 3D surface? The dominant answer to that question is an implicit function.
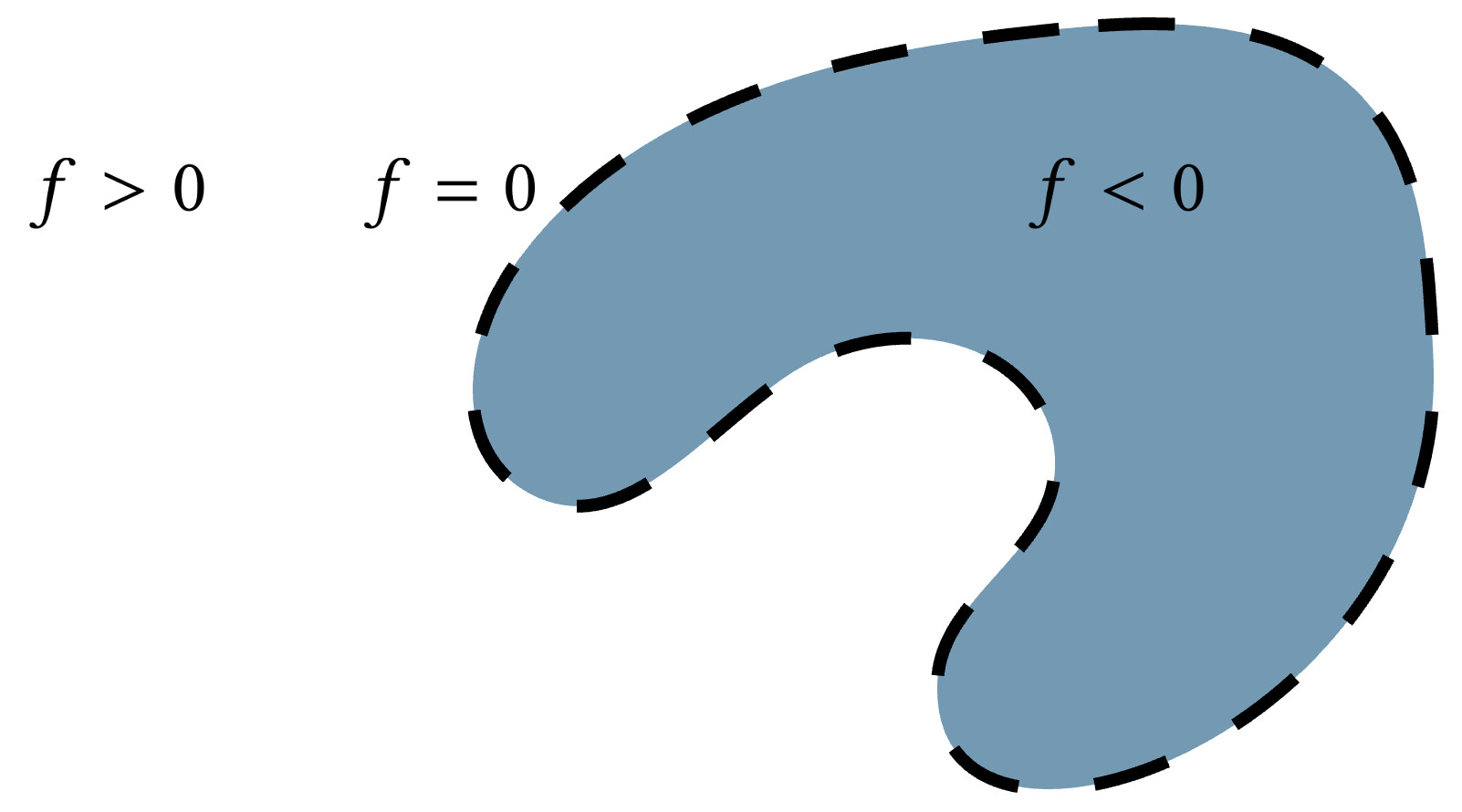
Beyond representing the surface as the zero level set of the function $f$, we can require extra criteria to make it a more powerful representation. We can say that besides being positive or negative when we're away from the surface, the magnitude of the function should also measure the distance to the surface. Equivalently, we could require that the function has a known Lipschitz bound (a mathy way of saying that we know it doesn't grow in value too quickly). This makes the implicit function $f$ a signed distance field (SDF) and really good for all sorts of geometric queries.
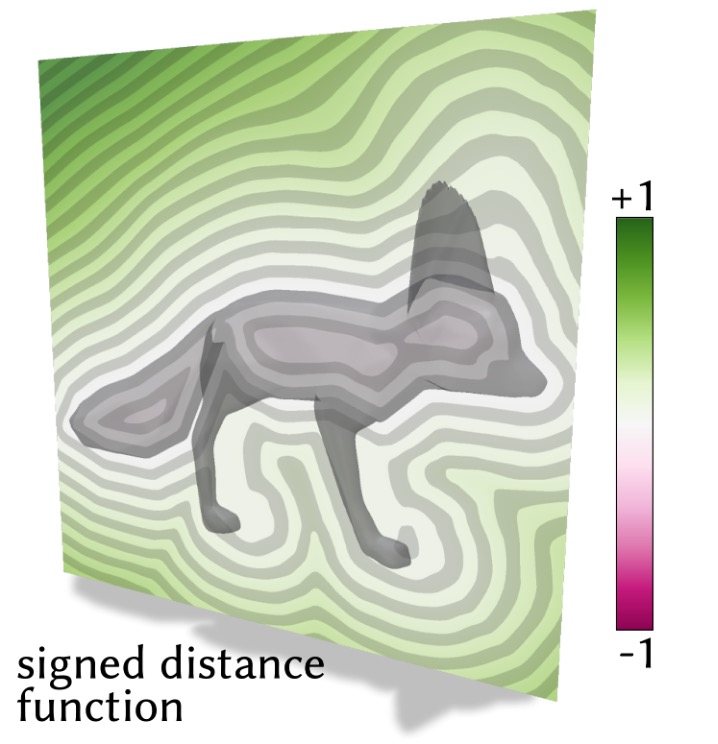
A basic operation we would like to conduct on 3D shapes is rendering. In terms of a query, this means we'd like to know whether a ray shot through a pixel hits the surface, how far away it hits the surface, and where on the surface it hits. We can use the distance property of the signed distance field to march along the ray until we find an intersection.
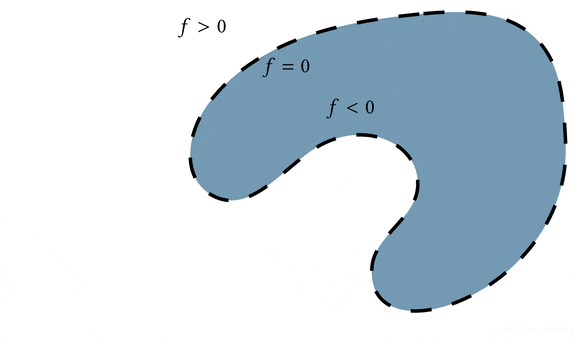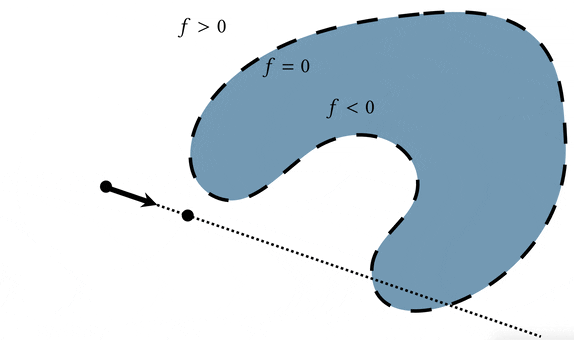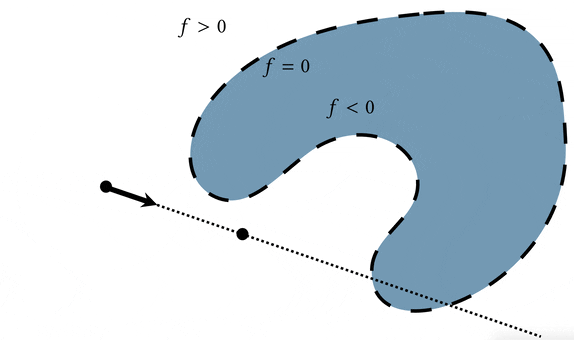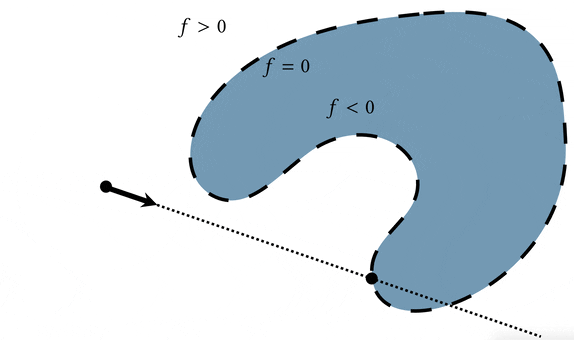
So far we haven't discussed how a signed distance field is actually stored on the computer. For simple shapes like spheres, we can just write down the mathematical formula for the signed distance field. Alternatively, we could try to build up complex shapes by composing signed distance fields of simple primitives. Or we could store signed distance values on a grid and interpolate them. We could even compute signed distances to a triangle mesh.
Neural networks enter the picture when we decide to parameterize a signed distance field $f$ with using a neural network: a "deep signed distance field" (Deep SDF). We pick an "architecture" for the neural network, consisting of layers of weights, non-linear activations. The input to the network are the $(x,y,z)$ coordinates of a point in space and the output is a single real number reporting or approximating the signed distance function at that point.
In the "DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation" [Park et al. 2019], the deep SDF function could be written as: $$(x,y,z,\mathbf{z}_i) \rightarrow f_\theta \rightarrow s$$ where $(x,y,z)$ is the query point, $\mathbf{z}_i$ is a latent code for the $i$th shape in the training dataset, $\theta$ are the shared weights of the neural network $f$, and $s$ is the output signed distance value.

Instead of thinking of the training process as outputting explicit representations of different shapes. We think of the training process as outputting a callable function that we can use inside of algorithms like sphere marching when conducting queries on the shape.
We can also train a specific neural network just to represent one shape. In this case, we don't have the latent code $\mathbf{z}_i$ as input and we indicate that the weights $\theta_i$ are optimized for a particular $i$th shape we might want to store: $$(x,y,z) \rightarrow f_{\theta_i} \rightarrow s.$$
From the point of view of training over an entire class of shapes, we can think of this as overfitting the network's weights to one particular shape. It's perhaps better to think of the training process as still "generalizing". We're just merely generalizing over all spacial queries $(x,y,z)$ and not also learning a distribution of shapes from a dataset.
This weight-based encoding can't easily do combinations between different shapes, but it gives us a very compact way to represent 3D shapes. Unlike storing a signed distance field on a grid, this neural network is able to adapt where it's spending its informational budget to the particular shape at hand.

We can also take the same neural network structure and train weights for each shape of a large dataset of shapes like Thingi10K to exploit this representation as a form of dataset compression. Since the non-linear space of functions is fixed by the network architecture, each shape is encoded as a simple vector of weight values.

Neural radiance fields (NeRFs) are similar to DeepSDFs or neural implicits. They are also taking a query point in space as input and outputting something related to geometry. Typically they're not outputting a signed distance field but rather a value $\sigma$ between zero and one representing a quantity more like occupancy or density of material in space and a quantity $(r,g,b)$ capturing color or reflectance of light: $$(x,y,z,\alpha,\beta) \rightarrow f_{\theta_i} \rightarrow (r,g,b,\sigma).$$ The weights $\theta_i$ represent a particular shape or scene and the additional inputs $\alpha$ and $\beta$ represent the viewing direction for reflectance calculations.
NeRFs have made it significantly easier to capture 3D scenes. Instead of representing a realistic 3D scene as a collection of triangle meshes with UV coordinates plus texture maps, we represent an entire scene by optimizing the weight values of a NeRF's neural network so that when we render the NeRF at each camera location it matches the corresponding photograph as closely as possible.
DeepSDFs and NeRFs show the power of neural fields for compression and reconstruction of 3D shapes, but we're also seeing their impact on modeling.
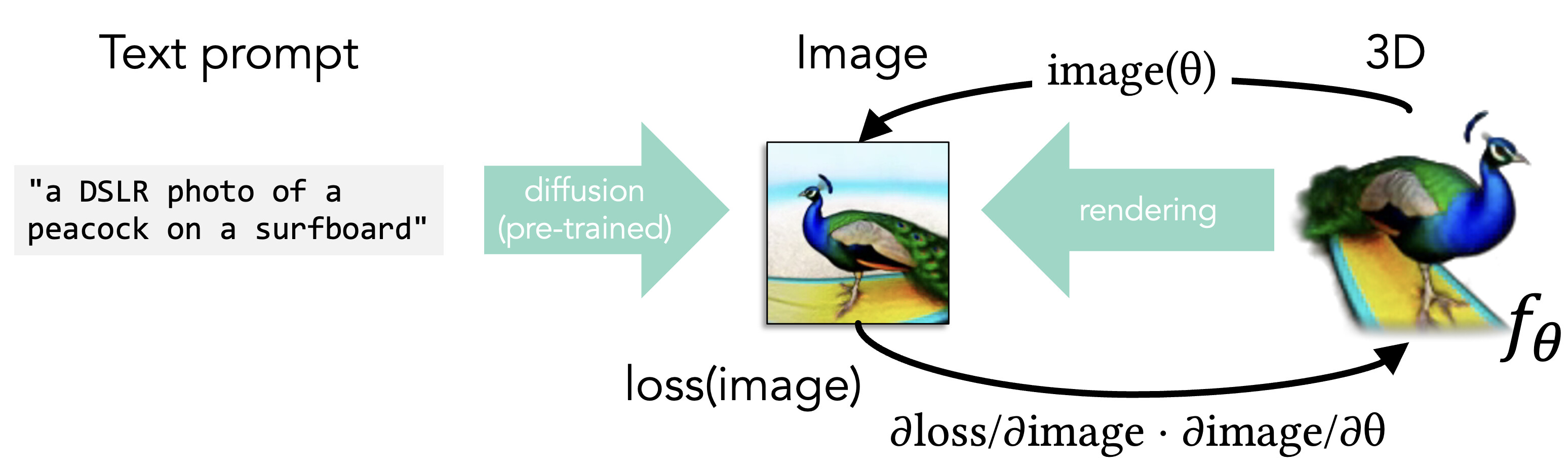
At a bird's eye view without getting into too many details, generative text-to-3D modeling works by taking a painfully expensive to train text-to-image diffusion model like stable diffusion. Something that takes all the images we have on the internet and boils them down into weights of a transformer and then can take a text prompt as input and repeatedly nudge an output image toward matching that text. We take our continuous 3D representation like a NeRF or DeepSDF with colors and we define the rendering function as a forward process that maps from the 3D world to the image domain.
Now, if we can measure a loss that tells us how well our rendered image matches the one predicted from the text prompt then we can pass the change in this loss function backwards to modify the 3D representation: via backpropagation. This requires that we can differentiate through the rendering process applying the chain rule so that the change in loss with respect to the image is pushed into change in the image with respect to the 3D representation. This works because NeRFs and DeepSDFs are a continuous parameterization of a big space of possible 3D shapes.
There are important details I've glossed over such as how to set up the loss to be sure you don't get a peacock pasted 10 times around your shape and that you actually descend in a quick manner (see for example "DreamFusion: Text-to-3D using 2D Diffusion" [Poole et al. 2022] or "Magic3D: High-Resolution Text-to-3D Content Creation" [Lin, Gao, Tang, Takikawa, Zeng, et al. 2023]).
Interestingly, the actual neural network part of these implicit 3D representations is not the essential ingredient. There are a number of papers (e.g., "ReLu Fields", "Plenoxels", or "Gaussian Splatting") in the last few years that just get rid of the neural network part in favor of some other non-linear implicit function parametrization.
The key ingredients appear to be: 1. a non-linear and continuous 3D representation; and 2. a differentiable process of going from the 3D representation to a 2D image (and 3. — as anyone knows who's actually done this — good camera alignment).
Compared to the simple diagram of arrows above, the triangle mesh pipeline suddenly appears quite stilted and complicated.

After many stages and lossy conversion processes we finally have something that looks like a production ready 3D asset that we could ship off to a computer game. The promise of this convoluted seeming pipeline is that once we're done then things like rendering and animation are incredibly fast and highly optimized for our current software and hardware stacks.
But this is not easy to optimize end-to-end. Suppose we wanted to take all the variables in this whole process and throw them into gradient descent. This would be really tricky. Many of the steps involve discrete choices and chain together sub-operations that don't necessarily talk well together. If our goal wasn't to create an asset for an existing 3D video game, then why are we doing it this way?
The triangle mesh pipeline has encouraged us to think of the space that we use for representing geometry as the same space that we use for doing computation on that geometry. We do this painful process of creating this triangle mesh, and then we think of that as the true surface that we're going to do our geometry processing on, and not only the true surface, but also this mesh must parameterize the space of anything we do on that surface.
My historical hypothesis is that when this pipeline really came into place both rendering and geometry processing were pretty slow and both kind of happy having fairly coarse 3D models.

Nowadays, both rendering and geometry processing are working with much higher resolution models. Nanite in the Unreal Engine gladly digests assets with millions or maybe even billions of triangles. Geometry processing research has found ways to scale up to million-triangle meshes (e.g., "Progressive Simulation for Cloth Quasistatics” [Zhang et al. 2022]). But yet, geometry processing methods primarily think of these triangle meshes in terms of defining all spaces that we're doing computation on as well.

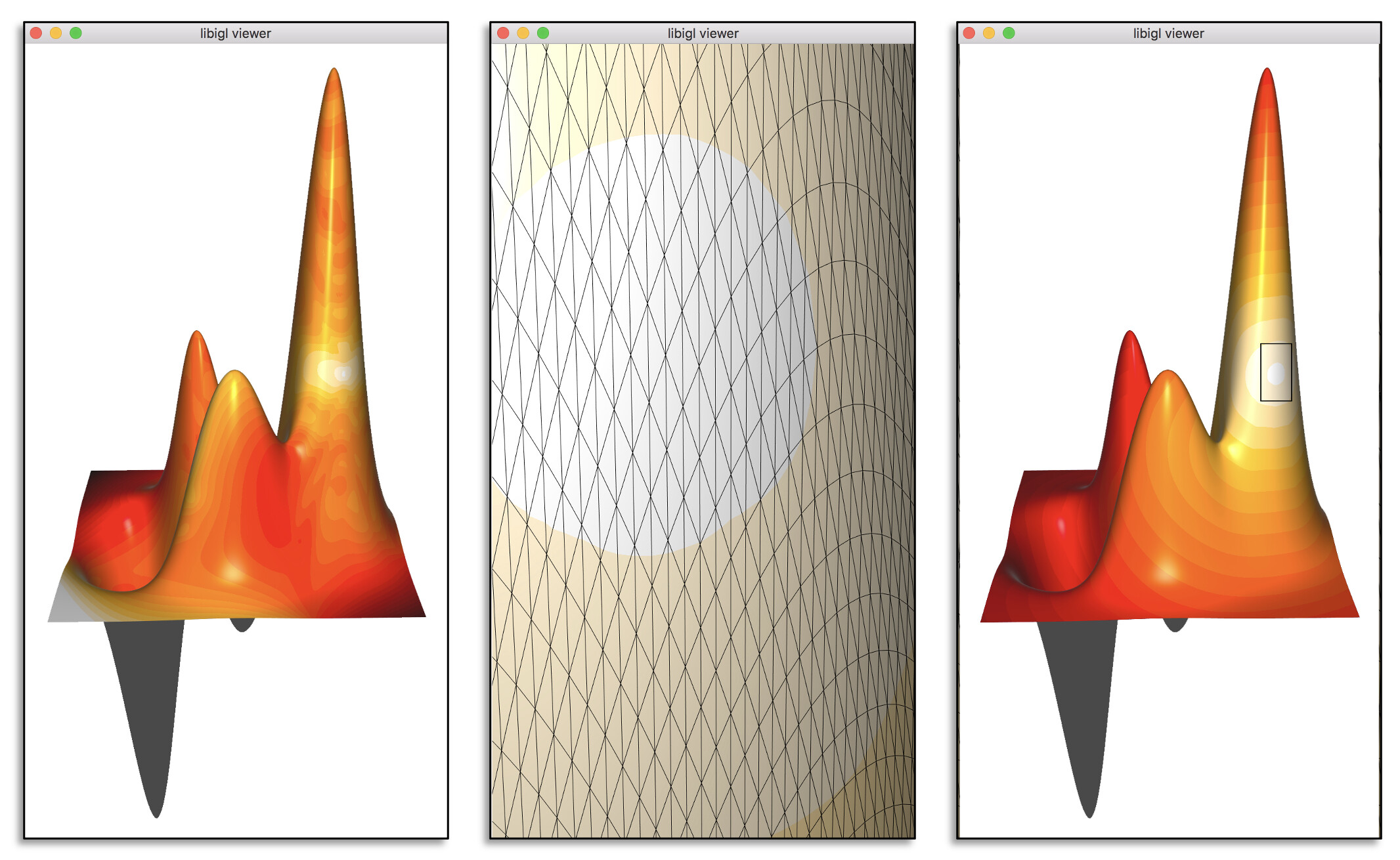
While long, skinny triangles are perfect for representing the geometry of the cylinder, if we also insist on using this mesh to represent all computation on the cylinder it means we can't represent interesting functions along the side of the cylinder. For example, we couldn't represent a wave rippling over the side of the cylinder. We've limited the function space to linear functions corresponding to the long edges.
We see the analogous problem happening with Gaussian splats. If I represent the cylinder with elongated Gaussian splats, they'll do a good job representing the side by putting very skewed or stretched Gaussians along the side.
For triangle meshes, the geometry processing community has an answer: intrinsic triangulations. We call a typical triangle mesh with vertex positions in 3D an extrinsic triangulation of a surface. Intrinsic triangulations build an alternative mesh over top an existing extrinsic triangulation.

Intrinsic triangulations are not a remeshing of the surface by adding new extrinsic triangles or vertices. And yet, we can represent much more interesting functions upon them.
Intrinsic triangulations are also a great way to improve the robustness of our algorithms, even on meshes that are high resolution.
Intrinsic remeshing comes at almost no extra cost. The world of intrinsic triangulations is becoming quite complete. As seen above, there is refinement and remeshing. There is also intrinsic simplification, which gives us a new way to navigate the quality performance trade-offs. If we want a solution faster while maintaining as much quality as we can, the old way was to simplify the geometry itself and then run our algorithm there, on the shared lower resolution function space. This results in much lower quality solutions than building a simplified intrinsic triangulation of the same resolution that lives atop the original surface without changing the geometry at all.
Intrinsic triangulations are an example — within the world of triangle meshes — showing the room to gain by embracing the diversity of function spaces. As new function spaces like NeRFs, DeepSDF, and Gaussian Splats flex their power for representation of geometry, we should learn from intrinsic triangulations not to blindly expect that these same representations will be ideal for computation.
So in year 2122, how will we represent 3D geometry? How will we do computation on 3D data? Will we keep triangle meshes for their explicitness? Or will we move completely to Gaussian splats and NeRFs for their fuzziness because they can represent surfaces that aren't smooth, hard surfaces.
My expectation is that we will move to representations that can leverage data in a meaningful way. That means moving away from rule-based representations. Looking back at the history of computer vision, this progression has been very clear.
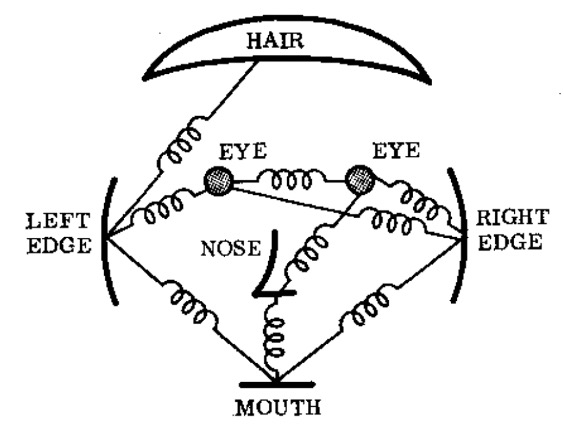
Rule-based models — like springs between face features — could be understood as a futile effort to model every possible interaction by hand: in vision, referred to disparagingly as hand-crafted features. Alternatively, they could be seen as an attempt to design a first-principles simulation of the underlying physics. But this is equally futile. For example, in the case of the human face, this would mean not just modeling the instantaneous elasto-dynamics and muscle activation in a face, but also the entire growth process resulting in that face. This may be a fun exercise in physics simulation for the sake of it, but it's not a promising way to do face detection.
Indeed, we have achieved astonishingly good face detection now by training models fed with billions of images of human faces. If those growth and movement physics are learned during that training, then they are latent or implicit in the model, not hard coded by rules. It was more promising to approximate the visual system than come up with a seemingly endless list of rules.
My hope for geometry processing is that by shifting to representations that separate geometric representation from computation we can similarly build better high-level applications. In particular, we should strive to build on representations that give us more insight into what comes before and after each step in the geometry processing pipeline.
Along with many others, I have worked much of my early career on making the geometry processing pipeline more robust. The idealized pipeline flushes input geometric data from acquisition through various stages of analysis and editing until consumption. In reality, we know that this pipeline suffers from various sources of "leaks".
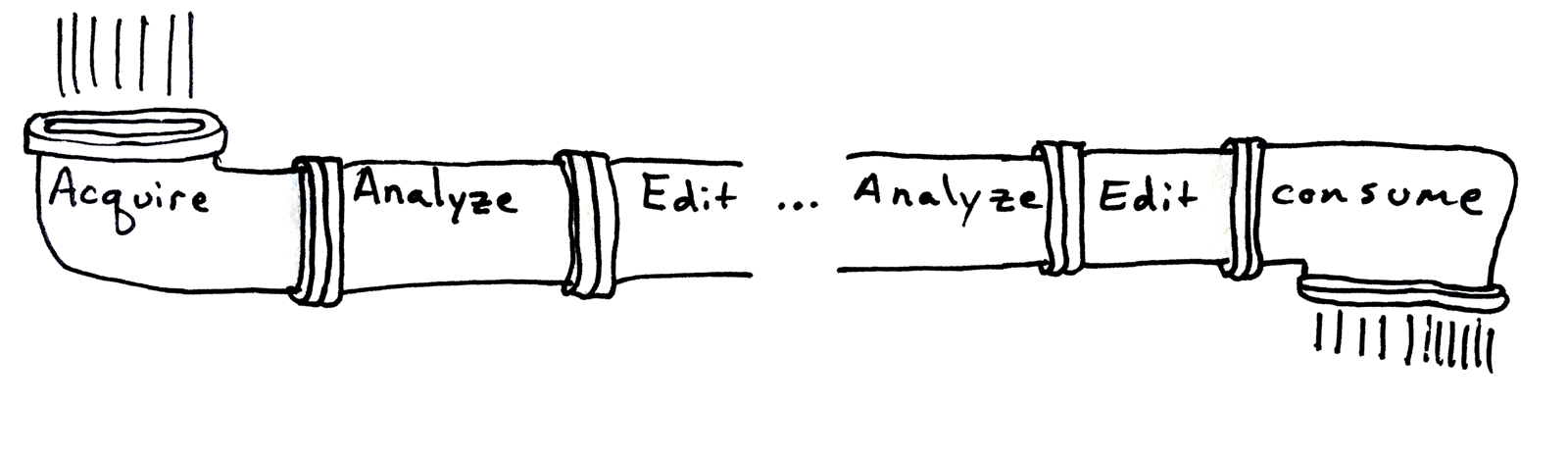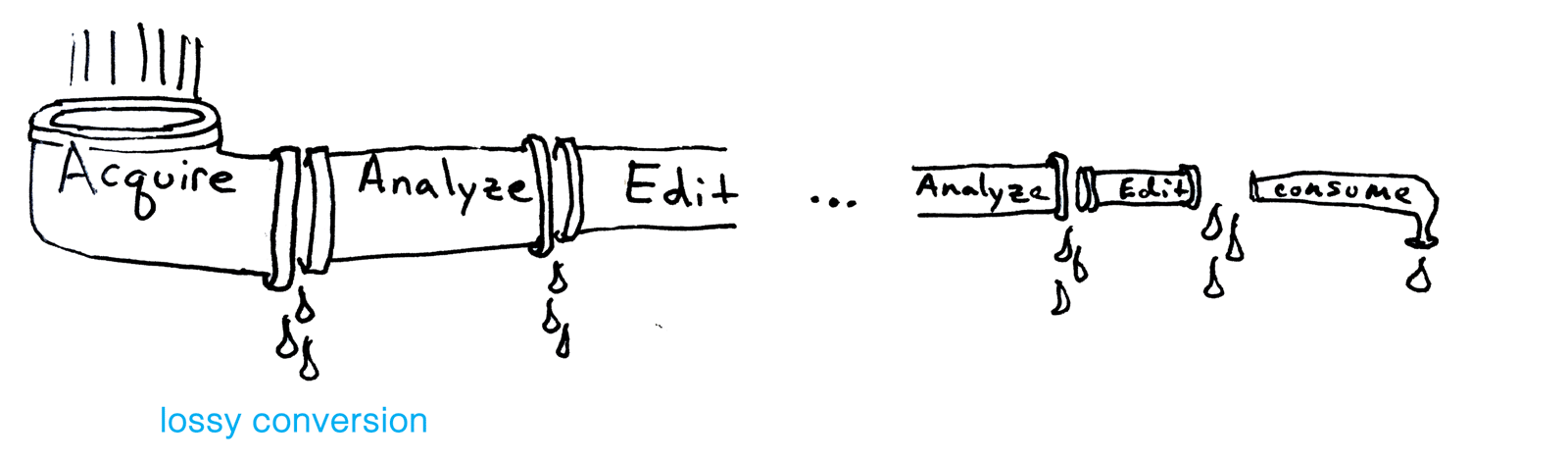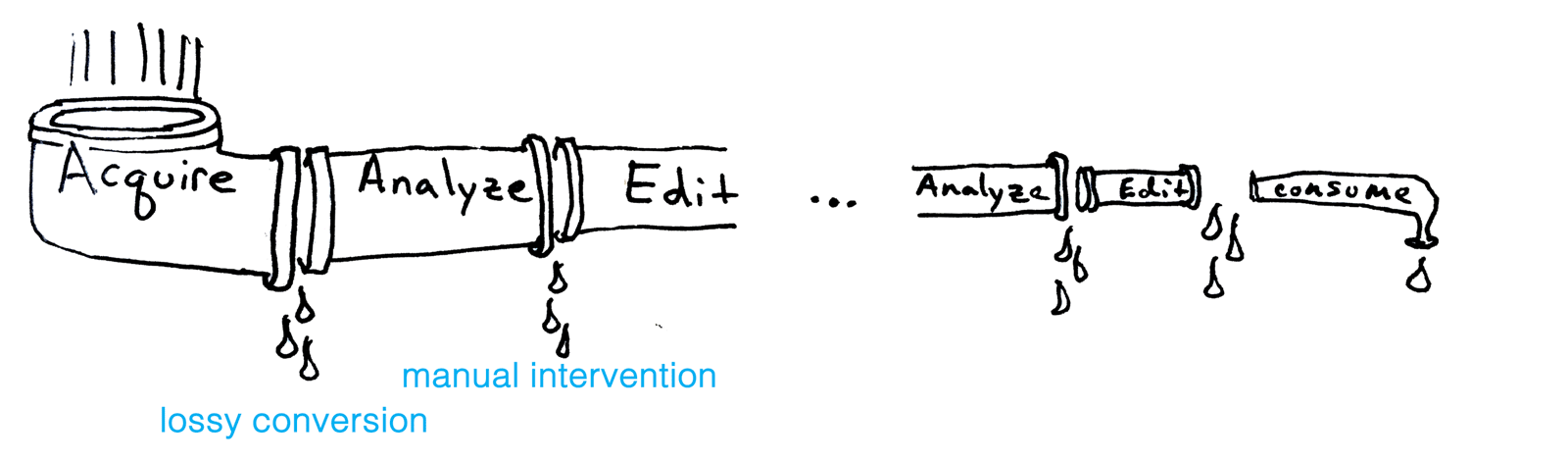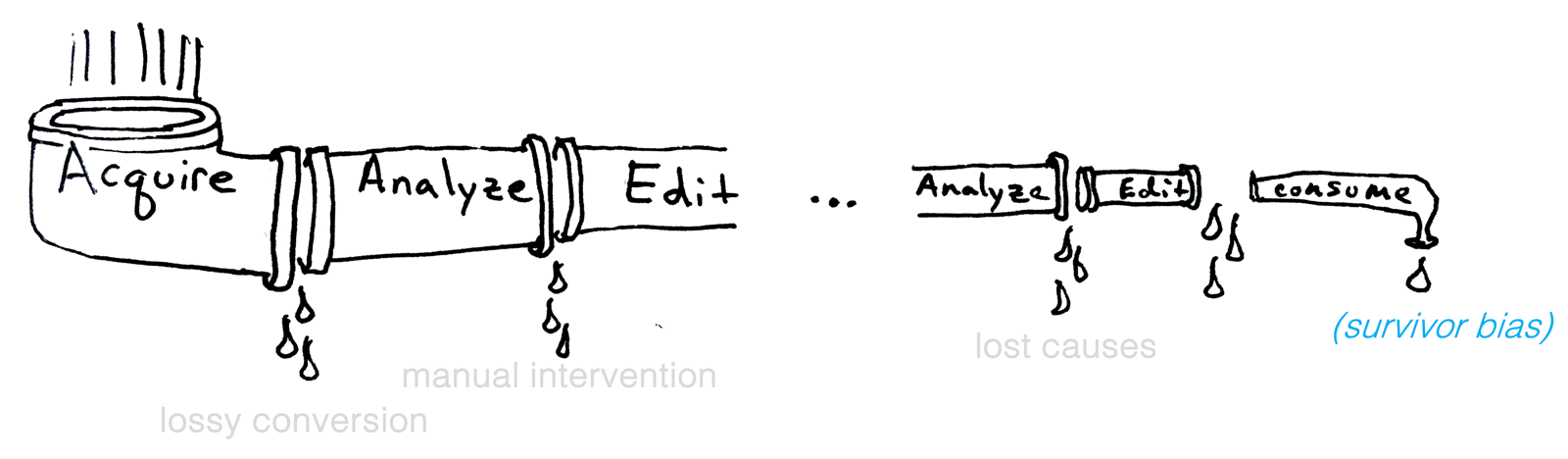
One of our most successful contributions to robust geometry processing was the concept of a generalized winding number, which was conceived originally as a subroutine in the process of conducting elastic simulation on a volumetric shape. In order to run finite-element simulation on a 3D shape, we needed a tetrahedralization of its interior. Existing tetrahedralization methods — like TetGen — were powerful but only if you told it where the inside versus the outside of the shape was: this is exactly what the generalized winding number could do. Once we could tetrahedralize any shape then we could join up with the rest of the simulation pipeline. We were plugging a hole in an existing pipeline.
Later, we realized that the generalized winding number was actually a way to skip over entire portions of geometry processing pipelines. Consider typical 3D printing software which expects as input a triangle mesh (really an .stl file) describing the surface of the shape to be printed.
If I have scanned some object into a point cloud, then I would need to first go through some process to create a triangle mesh, which I then hand off to the 3D printing software. Given this mesh, the software will decide for each slice through the object where the printer needs to squirt plastic to fill the interior of the shape. With respect to the original point cloud, this has just been a roundabout way of deciding what's inside and what's outside. Indeed, we can further generalize the winding number to point clouds to do just that.
Much of my past work has been on making geometry processing robust. I still think this is a noble pursuit. This improves the throughput of our geometry processing pipeline. But that's not enough!
I think we should question the pipeline altogether and specifically think about which parts of the pipeline have become obsolete, remaining only for legacy reasons.
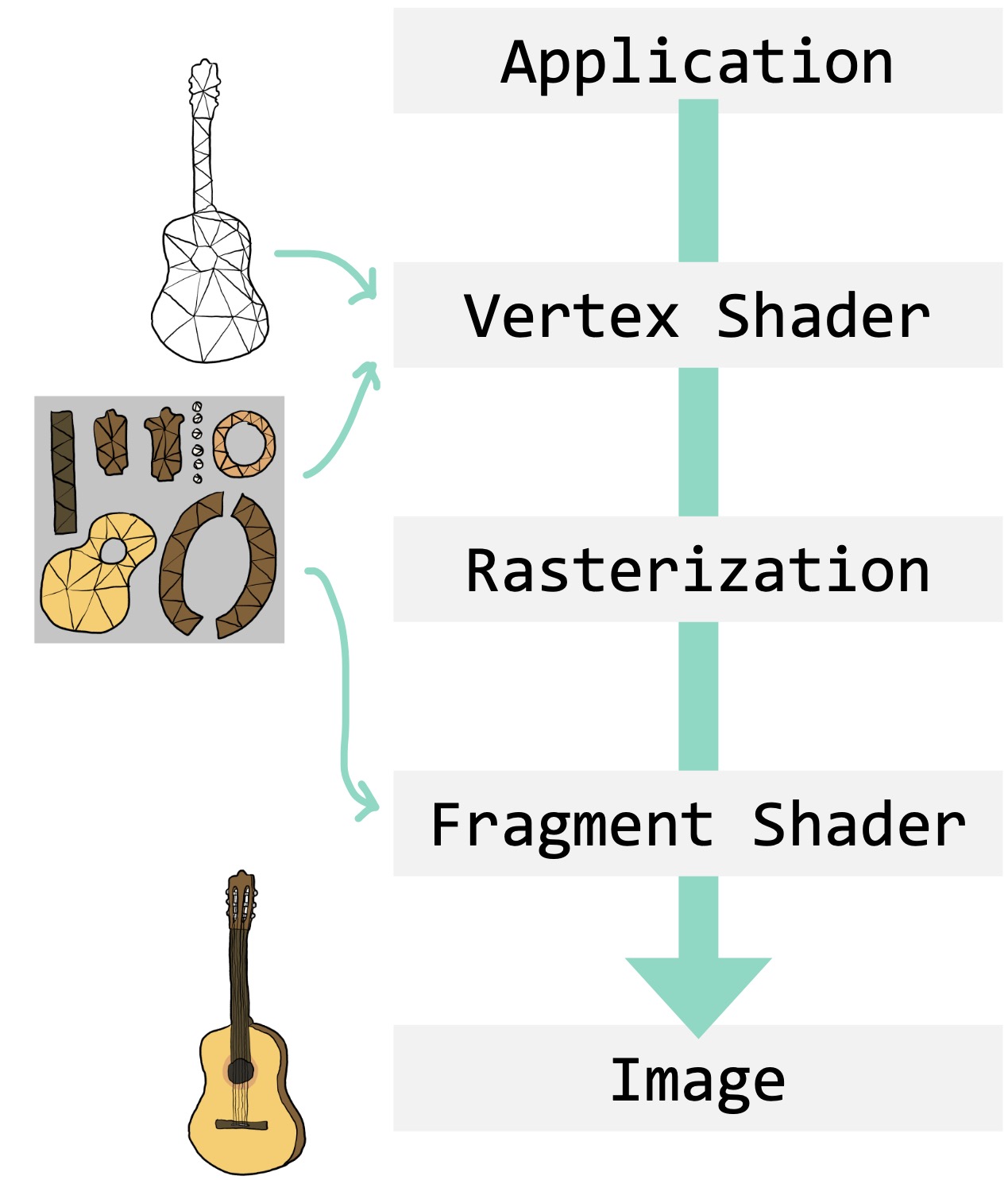
Consider storing colors for a 3D surface. The real-time rendering pipeline embraced texture mapping and geometry processing research responds with algorithms for automatic UV mapping. In turn, we typically think of this problem as picking new UV coordinates for each of the vertices of our mesh. Similarly, vertex shaders reposition vertices and we typically think of surface deformation as the problem of finding new positions over time for an existing triangle mesh's vertices.
Eventually, by assuming these problems should be posed this way, we also anchored our expectations that our algorithms should be solutions to tidy convex optimization problems and their performance should be roughly on the order of solving a big, sparse linear system. And then that biases the way that we judge new contributions in the field of geometry processing.
As researchers we should be more comfortable with the idea of doing gradient-based optimization, the dominant approach in machine learning.
It turns out even traditional mesh processing optimization problems can be solved more efficiently with the Adam solver. For example, both of the optimization problems in "Fast Quasi-Harmonic Weights for Geometric Data Interpolation" [Yu et al. 2021] and "Spectral Coarsening of Geometric Operators" [Liu et al. 2019] are convex programs that could be fed into black-box solvers. But each paper shows that you can get much better performance by running some variant of the Adam solver. We should break out of the habit of setting the goal as setting up a big linear system and solving it.
There's also lots waiting for us (e.g., "text-to-3D" as discussed above) if we're willing to spend the time and energy waiting for large, non-linear, perhaps less precisely defined optimization problems to converge (or at least "converge" in the machine learning sense). We should get more comfortable with problems that do not come equipped with simple mathematical checks for optimality.
Please don't get me wrong. Practitioners today definitely want triangles right now. Some practitioners see the advances of NeRF and Gaussian Splats as creating unusable clutter. They are "colorful flames" radiating their own light instead of reflecting light in a scene, simultaneously super high resolution while ultimately too noisy to extract a clean surface, and lacking part-based hierarchies needed for animation.
Practitioners with these complaints really don't want the current pipeline to change and would be really happy if we could continue making production-ready assets. And sure, this is also a worthy goal to pursue.
Ultimately, though, it's myopic to stick with the current triangle-mesh pipeline. We will limit ourselves to short-term gains. The problems may be safe, but they will be small.
Advances in topology optimization often output implicit functions which don't fit into the traditional CAD workflow. Imagine if we could instead change the downstream part of the pipeline to accept this output. Then, for example, the simulation or other verification process could not only seamlessly digest the output, but also have its criteria for success turned into a loss function that gets back propagated to affect the optimization end-to-end.
In 2001, Takeru Kobayashi shattered the hot dog eating contest raising the record from 25⅛ to 51 hot dogs in 12 minutes. At the time, other contests were simply trying to eat the next hot dog (in its bun) as quickly as possible. Instead, Kobayashi changed the pipeline and would devour the meat and bun separately, dunking the bun in water to swallow it whole. It's a wonderful, weird example of viewing the larger problem and optimizing for that or finding a new pattern that shatters the previous way of thinking about it.
Another way that I have been approaching problems is by asking, "am I solving a mesh problem or am I using a mesh to solve a problem?" The meshes are there for us. We don't owe them anything. We don't have to solve their problems. But we can use meshes to solve our problems.
Yet another guiding question is, "Are we looking for an exact solution to an approximate problem or an approximate solution to an exact problem?" Both questions frame research in an interesting way. Stereotypically, mathematicians approximate problems until they can be formulated precisely and if a solution is found, then it can be proven correct. In contrast, the stereotypical engineer might refine a heuristic solution to improve its performance on the actual problem facing people in reality. Both views have value, and we should find balance between them.
In the past, colleagues and I worked on the mesh Boolean problem. The inputs are triangles meshes, and we showed that if they meet certain generous criteria then we could give the precise answer to what their union or intersection is.

There was no arguing about whether we gave the right or the wrong answer if we accepted the framing of the problem. We could prove that it gave the correct result.
However, often what we want is not the pedantically exact result, but rather an approximate result to what we truly intended the problem to be.

Deriving or coding up an exact solution can be satisfying and feel mathematically rigorous. Relinquishing exactness to better approximate the real problem can be scientifically satisfying too. We don't have to see this point of view a less mathematical or less rigorous.
Colleagues and I have worked on tetrahedralization in the past. The leading tetrahedralization software preferred the "exact solution to the approximate problem" route: it would try its hardest to compute a tetrahedralization that exactly conformed to the triangles of an input surface mesh. The problem was that it would often fail and give no output. Instead, our approach preferred the "approximate solution to the exact problem" route. We allowed our tetrahedralization to remesh the surface as needed to guarantee that we would always output something. Once we always get some result, we can shift the discuss from binary failure rates, to statistical measures of quality, conformity to the input, etc. This naturally sets up a benchmark for future improvement along various axes.
For our SIGGRAPH North America 2011 submission, my advisor sent me an email with models and said something like, "Here are the models we can use." Those were the models back then.
In 2024, every result in your paper can be a different model. This is wonderful. You can go on stock websites like Thingiverse or TurboSquid and get the best model to make the point of a given research result. You can amass so many models that you can talk scientifically and statistically about the empirical performance of your algorithm versus the state of the art. You can find models that reflect the messiness of the real world, whether it's interesting high-resolution scans or meshes that come from modeling software that doesn't maintain all the nice things that keep our geometry processing algorithms working on clean data.
The messiness of geometric data will only increase. New reconstruction methods are going to flood the geometry processing pipeline with really nasty geometry. We should be ready for that. We should also admit when this messiness causes us to be unsure of an answer.
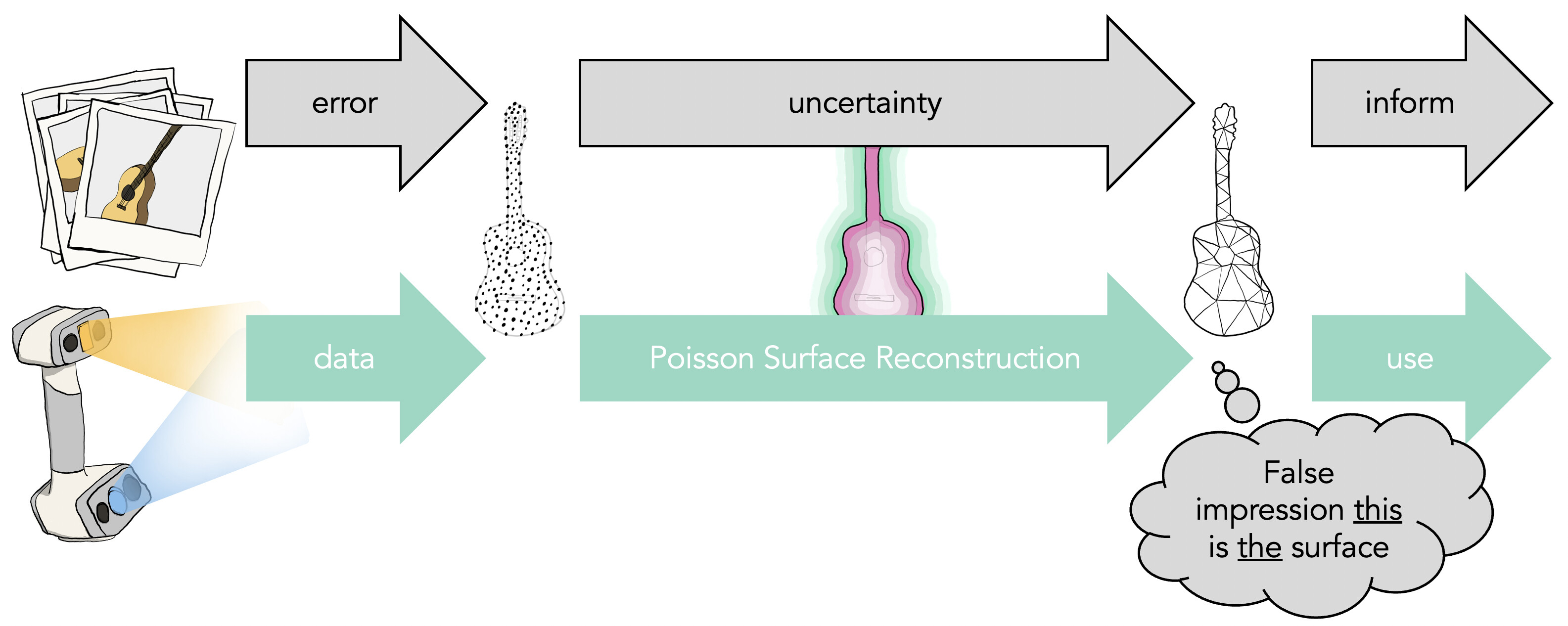
Meshes resulting from the reconstruction pipeline are just a particular output of a chain of algorithms that tried to make sense of the raw data that we captured. Instead, if we can track error through this process, it can turn into uncertainty accompanying answers along each step. This eventually turns into information that guides further downstream applications or directly informs people consuming the geometry.

We could reconstruct the geometry from a point cloud using a standard method like Poisson surface reconstruction. This method outputs a single shape that we could then test for collisions against.

Recently, a project lead by Silvia Sellán sought to equip the Poisson Surface Reconstruction method with statistically rich output.
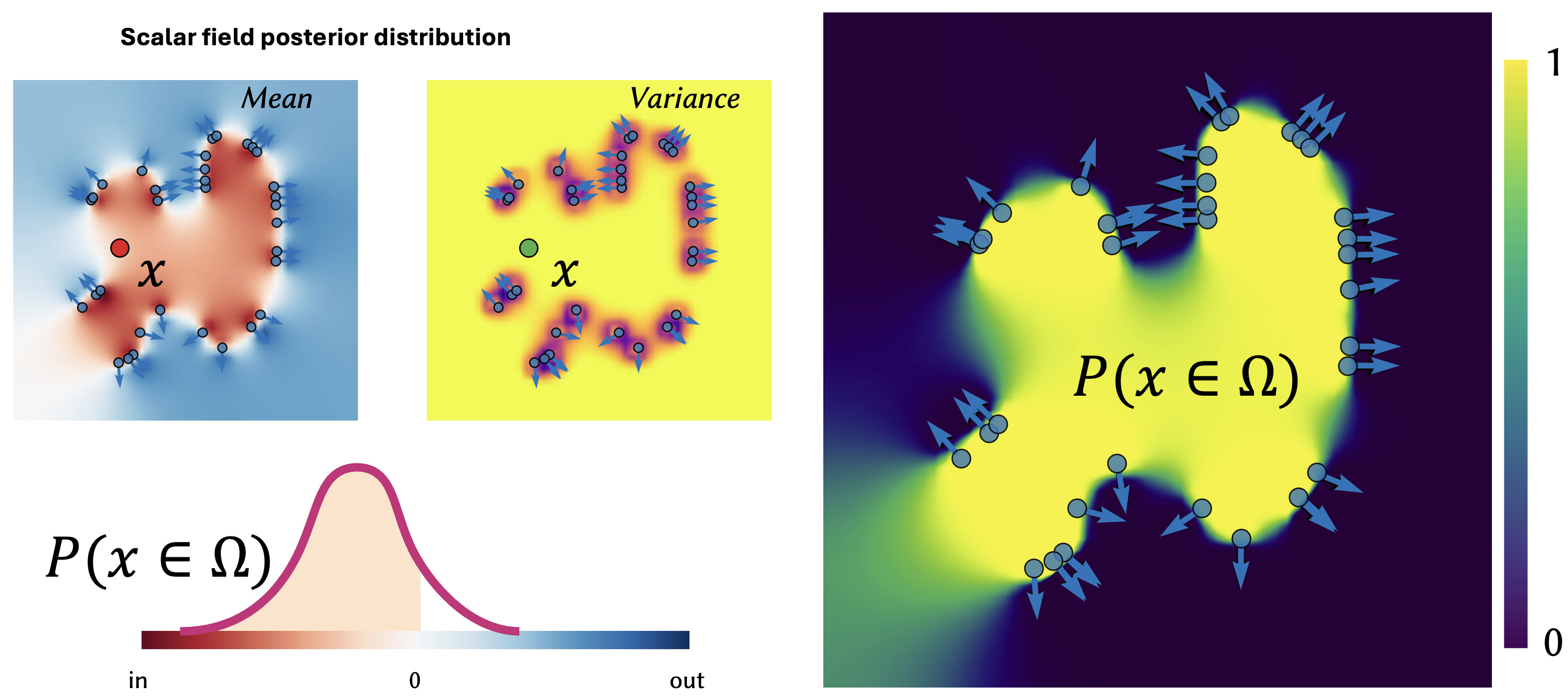
We can now ask what the probability is that the geometry covers any given point in space. This is a much more meaningful output than a single output geometry. We can take this idea of uncertainty and also apply it to novel representations, too.
One problem in the world of NeRF reconstructions occurs when you see part of the scene in only one of the input photographs. The easiest way for a NeRF to explain the blip is to put a little bit of colored density right in front of the camera for that photograph. We call these floaters. Karen X. Cheng's McDonald's ad playfully alludes to them, but generally we see them as a defect of the methodology.
"After AlexNet took first place in the ImageNet Challenge, everybody of a certain age went through the five stages of grief. First, there was shock and denial. It felt like the world was upended and nothing was going to be the same again. There was no denying the result, however."
— computer vision researcher, Michael Black
We see the same denial, anger, bargaining, and perhaps depression happening within some of the geometry processing community seeing new representations replace triangle meshes. Eventually, the computer vision community of course accepted deep learning and its success has been unparalleled. In geometry processing, our grief doesn't seem to be as deep and hopefully this eases our acceptance.
One frustrating thing is that we really care about geometry applications. Our community doesn't see them as simply tasks to apply machine learning to on one day, and move on to something else the next day. So, it's bittersweet to see machine learning advances make big, bold, messy progress on problems that we care so deeply about: procedural modeling, reconstruction, or even physical simulation.
In the end, the diversity of these representations in 3D are an opportunity for us. They allow us to tackle bigger portions of the geometry processing pipeline end-to-end. They open up bigger output spaces for our algorithms, including exciting things like uncertainty.
These will lead to much bigger impacts on people. This includes the professionals who care just as deeply about our applications as we do. Many of these professionals are outside of the world of visual effects, computer games and computer graphics, where we tracked the origins of our triangle mesh obsession.
Our progress in geometry processing stands to make a big impact on everyone on Earth. It's changing the way we do commerce, creation, and communication.
I would like to thank the collaborators on the projects I've referenced, including students: Benjamin Chislett, Gavin Barill, Hsueh-Ti Derek Liu, Jiayi Eris Zhang, Lily Goli, Mark Gillespie, Nicholas Sharp, Selena Ling, Silvia Sellán, Thomas Davies, Towaki Takikawa, Yixin Hu. I would also like to thank the authors of the works I've referenced, but was not involved in. Finally, I am fortunate to receive funding for my work at University of Toronto from NSERC, Sloan, Ontario ERA, Canada Research Chairs, Fields Institute, and gifts from Adobe.